19.2.2一次函数分段函数PPT格式课件下载.ppt

19.2.2一次函数分段函数PPT格式课件下载.ppt

《19.2.2一次函数分段函数PPT格式课件下载.ppt》由会员分享，可在线阅读，更多相关《19.2.2一次函数分段函数PPT格式课件下载.ppt（15页珍藏版）》请在冰豆网上搜索。

正比例函数吗？

你是怎样认为的？

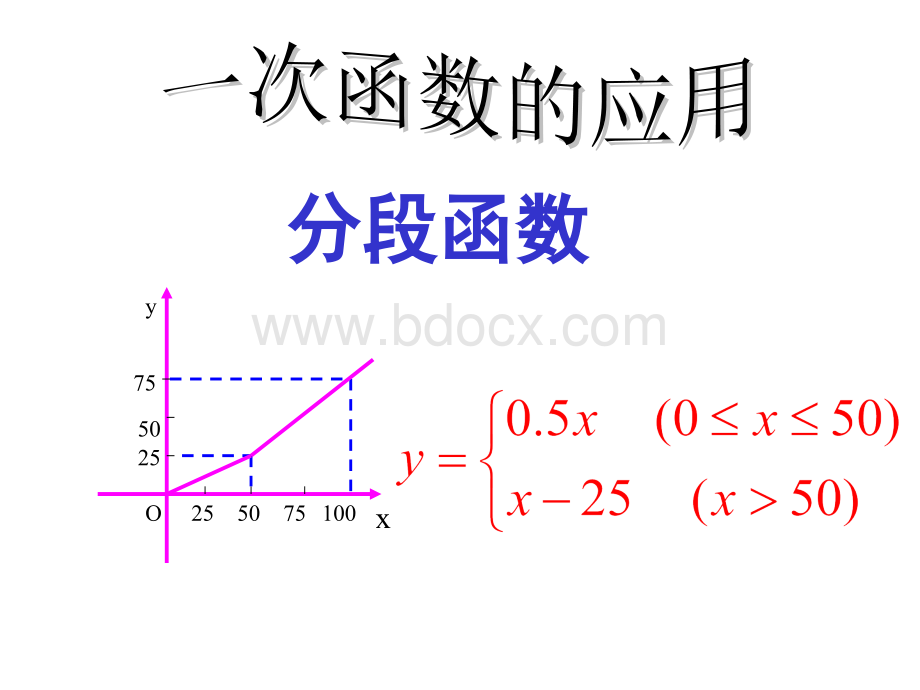
为了缓解用电紧张状况，某电力公司特制定了新的为了缓解用电紧张状况，某电力公司特制定了新的用电收费标准，每月用电用电收费标准，每月用电x（度）与应付电费（度）与应付电费y（元）（元）的关系如图所示。

的关系如图所示。

755025yOx755025100

（1）月用电量为）月用电量为50度时，应交电费度时，应交电费_元元;

25

（2）月用电量）月用电量x50度时，用电价格度时，用电价格是是_。

1元元/度度思考：

思考：

如何求出如何求出y与与x之间的函数关系式？

之间的函数关系式？

例例1为了缓解用电紧张状况，某电力公司特制定了新的为了缓解用电紧张状况，某电力公司特制定了新的用电收费标准，每月用电用电收费标准，每月用电x（度）与应付电费（度）与应付电费y（元）（元）的关系如图所示。

求出的关系如图所示。

求出y与与x之间的函数关系式？

755025yOx755025100解：

解：

当当0x50时时设设y与与x之间的函数关系式是之间的函数关系式是y=kx（k0）由题意，得由题意，得50k=25解得解得k=0.5y与与x之间的函数关系式是之间的函数关系式是y=0.5x当当x50时时设设y与与x之间的函数关系式是之间的函数关系式是y=mx+n（m0）由题意，得由题意，得50m+n=25100m+n=75解得解得m=1n=-25y与与x之间的函数关系式是之间的函数关系式是y=x-25为了缓解用电紧张状况，某电力公司特制定了新的为了缓解用电紧张状况，某电力公司特制定了新的用电收费标准，每月用电用电收费标准，每月用电x（度）与应付电费（度）与应付电费y（元）（元）的关系如图所示。

755025yOx755025100y与与x之间的函数关系式是之间的函数关系式是综上所述综上所述y=x-25y=y=0.5x（0x50）（x50）根据图象求分段函数的方法：

根据图象求分段函数的方法：

（1）观察图象，确定函数类型；

观察图象，确定函数类型；

（2）用待定系数法求解析式；

用待定系数法求解析式；

（3）注明各解析式自变量取值范围；

注明各解析式自变量取值范围；

归纳归纳例例2“黄金黄金1号号”玉米种子的价格为玉米种子的价格为5元元/千克，如果一千克，如果一次购买次购买2千克以上的种子，超过千克以上的种子，超过2千克的部分的种子千克的部分的种子的价格打的价格打8折。

折。

（1）填出下表填出下表:

购买种子的数购买种子的数量量/千克千克0.511.522.533.54付款金额付款金额/元元

（2）写出购买种子数量与付款金额之间的函数解析式写出购买种子数量与付款金额之间的函数解析式,并画出函数图象并画出函数图象2.557.5101214161851015100200300y/（米.分）x/分例例2小芳以小芳以200米米/分的速度起跑后，先匀加速跑分的速度起跑后，先匀加速跑5分，分，每分提高速度每分提高速度20米米/分，又匀速跑分，又匀速跑10分。

试写出这段时分。

试写出这段时间里她的跑步速度间里她的跑步速度y（单位：

米（单位：

米/分）随跑步时间分）随跑步时间x（单（单位：

分）变化的函数关系式，并画出函数图象。

位：

我们称此类我们称此类函数为分段函数为分段函数函数此函数图象是：

写分段函数解析式时，写分段函数解析式时，自变量的取值范围写在自变量的取值范围写在相应函数解析式的后面。

相应函数解析式的后面。

归纳归纳根据实际意义求分段函数的方法：

根据实际意义求分段函数的方法：

（1）分析文字，确定函数类型；

分析文字，确定函数类型；

（2）用列方程方法求解析式；

用列方程方法求解析式；

1.某市自来水公司为了鼓励市民节约用水，采取某市自来水公司为了鼓励市民节约用水，采取分段收费标准。

某户居民每月应交水费分段收费标准。

某户居民每月应交水费y（元元）是用水是用水量量x（吨吨）的函数，其图像如图：

的函数，其图像如图：

（1）分别写出分别写出x5时和和x5时，y与与x的函数解析式；

的函数解析式；

（2）观察察图像，利用函数解析式，回答自来水公司像，利用函数解析式，回答自来水公司采取的收采取的收费标准；

准；

（3）若某若某户该月用月用3吨，吨，则应交水交水费_元，若元，若该月交水月交水费12.5元，元，则用水用水_吨。

吨。

85X（吨吨）7.515y（元元）O2.某医药研究所开发一种新药，在试验药效时发现，如某医药研究所开发一种新药，在试验药效时发现，如果成人按规定剂量服用，那么服药两小时血液中含药量果成人按规定剂量服用，那么服药两小时血液中含药量最高，达到最高，达到6微克毫升（微克毫升（1微克微克103毫克），接着逐毫克），接着逐步衰减，步衰减，10小时的血液中含药量小时的血液中含药量3微克毫升，每毫升微克毫升，每毫升血液中含药量血液中含药量y（微克）随时间（微克）随时间x（小时）的变化如图所（小时）的变化如图所示示.当成人按规定服药后：

当成人按规定服药后：

分别求出当分别求出当x2和和x2时，时，y与与x之间的函数关系式之间的函数关系式.如果每毫升血液中含药量如果每毫升血液中含药量4微克或微克或4微克以上时在治疗疾病时是有效的，微克以上时在治疗疾病时是有效的，那么这个有效时间是多少？

那么这个有效时间是多少？

010326y（微克）（微克）X（小时小时）A3、如图，折线、如图，折线ABC是某地向北京打长途电话所是某地向北京打长途电话所需话费需话费y（元元）与通话时间与通话时间x（分分）之间的函数关系图。

之间的函数关系图。

x（分分）630y（元元）3.66ABC

（1）根据图象求出函数解析式；

根据图象求出函数解析式；

（2）求通话求通话2分钟所分钟所付话费付话费；

（3）求通话求通话5分钟所分钟所付话费付话费；

（4）若所付话费为若所付话费为9.2元，求通话时间。

元，求通话时间。

小结小结分段函数的求法分段函数的求法1、由实际意义求分段函数；

、由实际意义求分段函数；

2、由函数图象求分段函数；

、由函数图象求分段函数；

列方程方法列方程方法待定系数法待定系数法注意：

各段函数自变量取值范围各段函数自变量取值范围