届一轮复习人教A版43简单的三角恒等变换学案Word文件下载.docx
《届一轮复习人教A版43简单的三角恒等变换学案Word文件下载.docx》由会员分享,可在线阅读,更多相关《届一轮复习人教A版43简单的三角恒等变换学案Word文件下载.docx(17页珍藏版)》请在冰豆网上搜索。
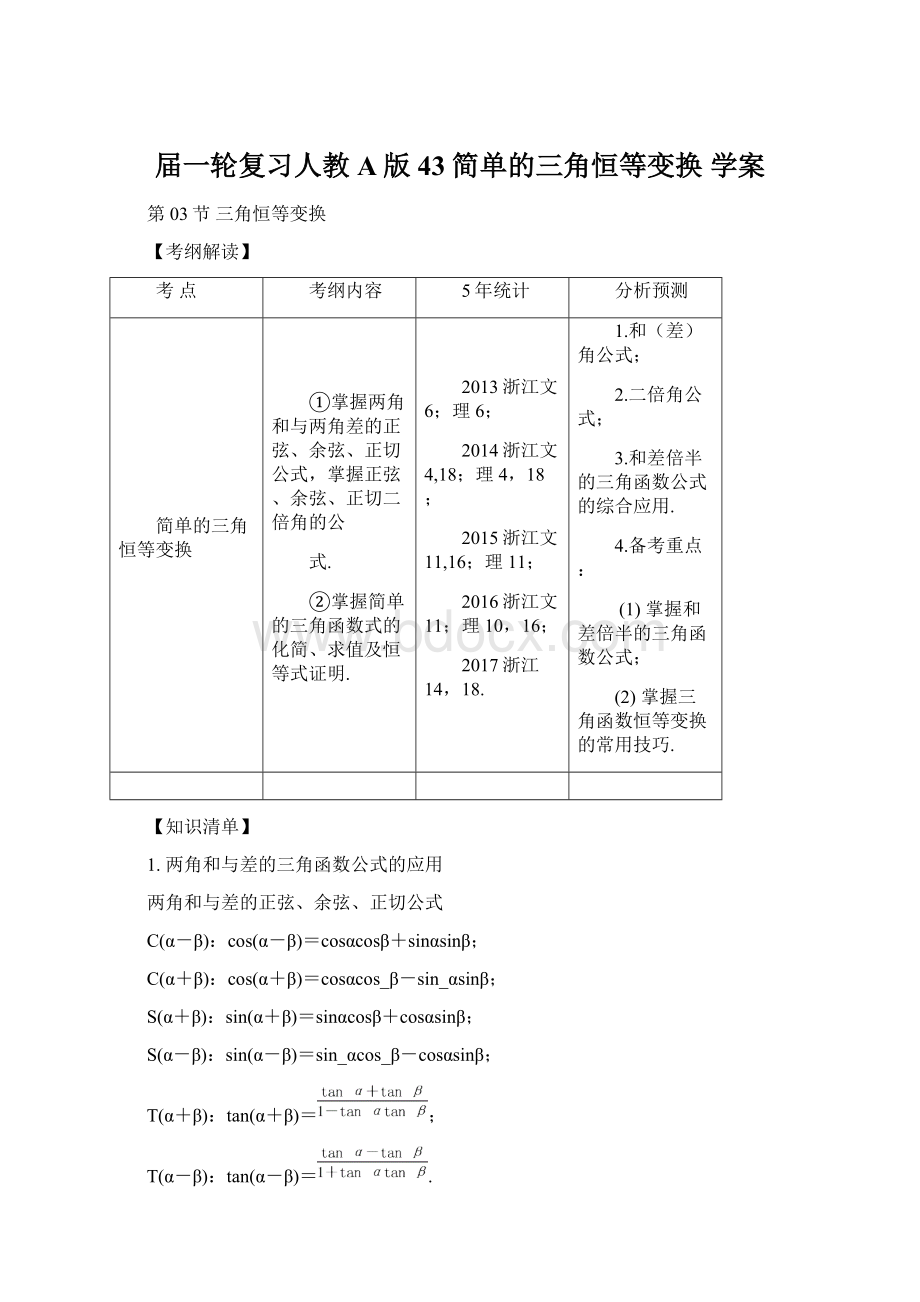
4.备考重点:
(1)掌握和差倍半的三角函数公式;
(2)掌握三角函数恒等变换的常用技巧.
【知识清单】
1.两角和与差的三角函数公式的应用
两角和与差的正弦、余弦、正切公式
C(α-β):
cos(α-β)=cosαcosβ+sinαsinβ;
C(α+β):
cos(α+β)=cosαcos_β-sin_αsinβ;
S(α+β):
sin(α+β)=sinαcosβ+cosαsinβ;
S(α-β):
sin(α-β)=sin_αcos_β-cosαsinβ;
T(α+β):
tan(α+β)=;
T(α-β):
tan(α-β)=.
变形公式:
tanα±
tanβ=tan(α±
β)(1∓tanαtanβ);
.
函数f(α)=acosα+bsinα(a,b为常数),可以化为f(α)=sin(α+φ)或f(α)=cos(α-φ),其中φ可由a,b的值唯一确定.
对点练习:
【2018广西南宁二中、柳州高中9月联考】若,且为第三象限角,则等于()
A.7B.C.1D.0
【答案】A
本题选择A选项.
2.二倍角公式的运用公式的应用
二倍角的正弦、余弦、正切公式:
S2α:
sin2α=2sin_αcos_α;
C2α:
cos2α=cos2α-sin2α=2cos2α-1=1-2sin2α;
T2α:
tan2α=.
cos2α=,sin2α=
1+sin2α=(sinα+cosα)2,1-sin2α=(sinα-cosα)2
【2017浙江,18】已知函数f(x)=sin2x–cos2x–sinxcosx(xR).
(Ⅰ)求的值.
(Ⅱ)求的最小正周期及单调递增区间.
【答案】
(Ⅰ)2;
(Ⅱ)最小正周期为,单调递增区间为.
【解析】
(Ⅱ)由与得
所以的最小正周期是
由正弦函数的性质得
解得
所以的单调递增区间是.
【考点深度剖析】
对于三角恒等变换,高考命题主要以公式的基本运用、计算为主,其中多以与角的范围、三角函数的性质、三角形等知识结合考查,在三角恒等变换过程中,准确记忆公式、适当变换式子、有效选取公式是解决问题的关键.
【重点难点突破】
考点1两角和与差的三角函数公式的应用
【1-1】【2018江西省赣州厚德外国语学校上学期第一次测试】的值是()
A.B.C.D.
【答案】D
【解析】故选D.
【1-2】【2018河南省名校联盟第一次段考】已知圆:
,点,,记射线与轴正半轴所夹的锐角为,将点绕圆心逆时针旋转角度得到点,则点的坐标为__________.
【解析】设射线OB与轴正半轴的夹角为,有已知有,所以,且,C点坐标为.
【1-3】已知:
,,且,则=_______.
【解析】,
【领悟技法】
1.运用两角和与差的三角函数公式时,不但要熟练,准确,而且要熟悉公式的逆用及变形,如tanα+tanβ=tan(α+β)·
(1-tanαtanβ)和二倍角的余弦公式的多种变形等.
2.应熟悉公式的逆用和变形应用,公式的正用是常见的,但逆用和变形应用则往往容易被忽视,公式的逆用和变形应用更能开拓思路,培养从正向思维向逆向思维转化的能力,只有熟悉了公式的逆用和变形应用后,才能真正掌握公式的应用.
提醒:
在T(α+β)与T(α-β)中,α,β,α±
β都不等于kπ+(k∈Z),即保证tanα,tanβ,tan(α+β)都有意义;
若α,β中有一角是kπ+(k∈Z),可利用诱导公式化简.
【触类旁通】
【变式一】已知均为锐角,且,.
(Ⅰ)求的值;
(Ⅱ)求的值.
∴.
【变式二】已知函数的部分图像如图所示.
(Ⅰ)求函数)的解析式,并写出的单调减区间;
(Ⅱ)的内角分别是A,B,C.若,,求的值.
(Ⅰ)由图象最高点得A=1,
由周期.
当时,,可得,
因为,所以.
.
由图象可得的单调减区间为.
考点2二倍角公式的运用公式的应用
【2-1】【2017浙江ZDB联盟一模】已知,,则__________,__________.
【答案】
【解析】因为,,所以
因为,所以,因此.
【2-2】【江苏省淮安市五模】已知,且,则的值为.
【2-3】已知,且,则的值为__________.
【解析】因为,所以,,,又因为,所以.
三角函数式的化简要遵循“三看”原则:
(1)一看“角”,通过看角之间的差别与联系,把角进行合理的拆分,从而正确使用公式;
(2)二看“函数名称”,看函数名称之间的差异,从而确定使用的公式;
(3)三看“结构特征”,分析结构特征,找到变形的方向.
【变式一】已知,
(1)求的值;
(2)求的值.
【变式二】已知,,则的值为()
A.B.C.D.
【解析】由二倍角公式得,整理得,
因此,由于,,,
,故答案为A.
考点3三角恒等式的证明
【3-1】求证:
=sin2α.
【解析】∵左边====
=cosαsincos=sinαcosα
=sin2α=右边.
∴原式成立.
【3-2】求证:
=-2cos(α+β).
【3-3】已知,,且,.
证明:
【解析】,即,
,
又,,
,,,
1.三角恒等式的证明主要有两种类型:
绝对恒等式与条件恒等式.
(1)证明绝对恒等式要根据等式两边的特征,化繁为简,左右归一,变更论证,通过三角恒等式变换,使等式的两边化异为同.
(2)条件恒等式的证明则要认真观察,比较已知条件与求证等式之间的联系,选择适当途径.常用代入法、消元法、两头凑等方法.
(3)变角:
目的是沟通题设条件与结论中所涉及的角,其手法通常是“配凑”.变名:
通过变换函数名称达到减少函数种类的目的,其手法通常有“切化弦”、“升幂与降幂”等.
2.变换技巧:
(1)拆角、拼角技巧:
2α=(α+β)+(α-β);
β=-;
=.
(3)化简技巧:
切化弦、“1”的代换等
【变式一】求证:
【解析】左边=+
故原式得证.
【变式二】已知,证明:
【解析】左边
右边.
故原命题成立.
考点4三角函数的综合应用
【4-1】【2018湖北省部分重点中学起点】设函数,其中θ∈,则导数f′
(1)的取值范围是________.
【答案】[,2]
【4-2】【2017浙江温州二模】已知函数.
(1)求函数的最小正周期;
(2)若,,求的值.
(1);
(2).
【解析】试题解析:
(1)
∴函数的最小正周期是
(2)∴,
,∴,又.
∴∴,
∴.
【4-3】【2018江苏海安上学期第一次测试】已知向量,,.
(1)若,求的值;
(2)记,求的最大值和最小值以及对应的的值.
(1);
(2)当时,取到最大值3;
当时,取到最小值..
【解析】试题分析:
(1)依据题设条件建立方程分析求解;
(2)先运用向量的坐标形式的数量积公式建立函数,然后借助余弦函数的图像和性质进行探求:
解:
(1)因为,,,
所以.
若,则,与矛盾,故.
于是.
又,所以.
【领悟技法】高考对两角和与差的正弦、余弦、正切公式及二倍角公式的考查还往往渗透在研究三角函数性质中.需要利用这些公式,先把函数解析式化为的形式,再进一步讨论其定义域、值域和最值、单调性、奇偶性、周期性、对称性等性质.
【变式一】【2017浙江湖州、衢州、丽水三市4月联考】函数的部分图象如图所示,M为最高点,该图象与y轴交于点,与x轴交于点B,C,且的面积为.
(Ⅰ)求函数的解析式;
(Ⅱ)若,求的值.
(Ⅰ);
(Ⅱ).
试题解析:
(Ⅰ)因为,
所以周期,,
由,得,
因为,所以,
所以;
(Ⅱ)由,得,
【易错试题常警惕】
易错典例:
若sinθ,cosθ是关于x的方程5x2-x+a=0(a是常数)的两根,θ∈(0,π),求cos2θ的值.
易错分析:
不注意挖隐含条件,角的取值范围,处理好开方、平方关系,避免出现增解与漏解的错误.
正确解析:
由题意知:
sinθ+cosθ=,
温馨提醒:
求解三角函数问题,应灵活运用公式,特别注意已知等式中角的取值范围,涉及开方求值问题,注意正负号的选取.
【学科素养提升之思想方法篇】
数形结合百般好,隔裂分家万事休——数形结合思想
我国著名数学家华罗庚曾说过:
"
数形结合百般好,隔裂分家万事休。
数"
与"
形"
反映了事物两个方面的属性。
我们认为,数形结合,主要指的是数与形之间的一一对应关系。
数形结合就是把抽象的数学语言、数量关系与直观的几何图形、位置关系结合起来,通过"
以形助数"
或"
以数解形"
即通过抽象思维与形象思维的结合,可以使复杂问题简单化,抽象问题具体化,从而起到优化解题途径的目的.
向量的几何表示,三角形、平行四边形法则,使向量具备形的特征,而向量的坐标表示和坐标运算又具备数的特征,因此,向量融数与形于一身,具备了几何形式与代数形式的“双重身份”.因此,在应用向量解决问题或解答向量问题时,要注意恰当地运用数形结合思想,将复杂问题简单化、将抽象问题具体化,达到事半功倍的效果.
【典例】在平面坐标系中,直线与圆相交于,(在第一象限)两个不同的点,且则的值是()
A.B.C.D.
∴.