新的抗震规范将结构分为规则结构一般不规则结构特别不规则结构和严重不规则结构而严重不规则结构是禁Word文档格式.docx

新的抗震规范将结构分为规则结构一般不规则结构特别不规则结构和严重不规则结构而严重不规则结构是禁Word文档格式.docx

《新的抗震规范将结构分为规则结构一般不规则结构特别不规则结构和严重不规则结构而严重不规则结构是禁Word文档格式.docx》由会员分享，可在线阅读，更多相关《新的抗震规范将结构分为规则结构一般不规则结构特别不规则结构和严重不规则结构而严重不规则结构是禁Word文档格式.docx（54页珍藏版）》请在冰豆网上搜索。

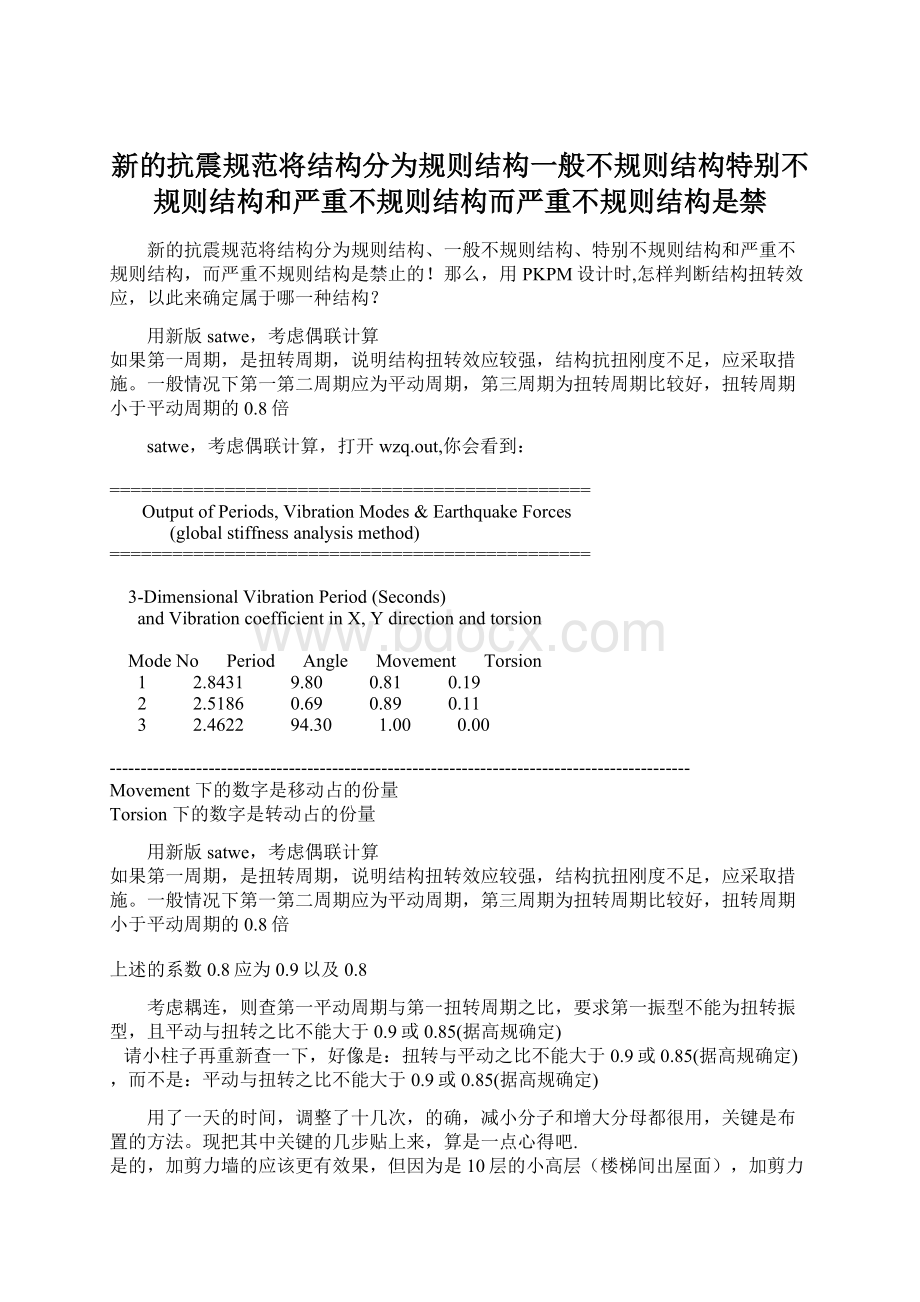
EarthquakeForces

（globalstiffnessanalysismethod）

3-DimensionalVibrationPeriod（Seconds）

andVibrationcoefficientinX,Ydirectionandtorsion

ModeNo　Period　Angle　Movement　Torsion

1　　2.8431　　9.80　　0.81　　0.19

2　　2.5186　　0.69　　0.89　　0.11

3　　2.4622　　94.30　　1.00　　0.00

----------------------------------------------------------------------------------------------

Movement下的数字是移动占的份量

Torsion下的数字是转动占的份量

一般情况下第一第二周期应为平动周期，第三周期为扭转周期比较好，扭转周期小于平动周期的0.8倍

上述的系数0.8应为0.9以及0.8

考虑耦连，则查第一平动周期与第一扭转周期之比，要求第一振型不能为扭转振型，且平动与扭转之比不能大于0.9或0.85（据高规确定）

请小柱子再重新查一下，好像是：

扭转与平动之比不能大于0.9或0.85（据高规确定），而不是：

平动与扭转之比不能大于0.9或0.85（据高规确定）

用了一天的时间，调整了十几次，的确，减小分子和增大分母都很用，关键是布置的方法。

现把其中关键的几步贴上来，算是一点心得吧.

是的，加剪力墙的应该更有效果，但因为是10层的小高层（楼梯间出屋面），加剪力墙造价势必增加很大，所以，就采用的框架结构。

1.最初的周期值：

振型号周期转角平动系数（X+Y）扭转系数

11.455189.711.00（0.00+1.00）0.00

21.4224179.360.68（0.68+0.00）0.32

31.36210.460.32（0.32+0.00）0.68

Tt/t1=1.3621/1.4551=0.93

2.调整部分边柱：

500*500---600*600

11.44511.890.91（0.91+0.00）0.09

21.441491.791.00（0.00+1.00）0.00

31.33430.830.09（0.09+0.00）0.91

Tt/t1=1.3343/1.4451=0.92

3.调整中部梁：

250*500----250*400

11.534589.851.00（0.00+1.00）0.00

21.4584179.570.72（0.72+0.00）0.28

31.38270.540.28（0.28+0.00）0.72

Tt/t1=1.3827/1.5345=0.90

4。

部分中部梁超筋，加大截面，调整部分边梁,边柱：

11.455189.811.00（0.00+1.00）0.00

21.4044179.690.86（0.86+0.00）0.14

31.30460.550.14（0.14+0.00）0.86

Tt/t1=1.3046/1.4551=0.89

======================================================================

周期、地震力与振型输出文件

（侧刚分析方法）

考虑扭转耦联时的振动周期（秒）、X,Y方向的平动系数、扭转系数

11.4877179.670.99（0.99+0.00）0.01

21.440461.260.02（0.01+0.02）0.98

31.059990.240.98（0.00+0.98）0.02

40.4531179.891.00（1.00+0.00）0.00

50.434873.560.02（0.00+0.02）0.98

60.283790.170.98（0.00+0.98）0.02

70.23680.371.00（1.00+0.00）0.00

80.2239104.570.01（0.00+0.01）0.99

90.15160.890.99（0.99+0.00）0.01

100.1399110.220.05（0.01+0.04）0.95

110.134690.270.96（0.00+0.96）0.04

120.10781.140.97（0.96+0.00）0.03

130.0972158.040.04（0.04+0.01）0.96

140.084090.300.99（0.00+0.99）0.01

150.08221.210.94（0.94+0.00）0.06

地震作用最大的方向=0.216（度）

是不是第2就是扭转为主的第一自振周期Tt，第1就是平动为主的第一自振周期T1，还是要“平动系数（X+Y）”=1.00（1.00+0.00）才行？

周期比，位移比是通过数据来分析结构布置的合理性，另外更重要的是强调抗震概念设计，避免极不规则的结构体系！

实际工程中常常扭转效应较大，原则是离刚心越远的地方增加抗侧力构件的刚度，可调整边框梁柱，剪力墙断面。

同时可减小X,Y向侧向刚度，总之Tt/T1,从分母，分子两个方面着手即可。

另外，多层只需满足抗规的要求，只有位移比控制，没有周期比控制，但可参考分析。

有关振型的几个概念

振型参与系数：

每个质点质量与其在某一振型中相应坐标乘积之和与该振型的主质量（或者说该模态质量）之比，即为该振型的振型参与系数。

一阶振型自振频率最小（周期最长）,二阶,三阶....振型的自振频率逐渐增大.地震力大小和地面加速度大小成正比,周期越长加速度越小,地震力也越小。

自振振型曲线是在结构某一阶特征周期下算得的各个质点相对位移（模态向量）的图形示意.在形状上如实反映实际结构在该周期下的振动形态.振型零点是指在该振型下结构的位移反应为0。

振型越高，周期越短，地震力越大，但由于我们地震反应是各振型的迭代，高振型的振型参与系数小。

特别是对规则的建筑物，由于高振型的参与系数小，一般忽略高振型的影响。

振型的有效质量：

这个概念只对于串连刚片系模型有效（即基于刚性楼板假定的，不适用于一般结构。

）。

某一振型的某一方向的有效质量为各个质点质量与该质点在该一振型中相应方向对应坐标乘积之和的平方。

一个振型有三个方向的有效质量，而且所有振型平动方向的有效质量之和等于各个质点的的质量之和，转动方向的有效质量之和等于各个质点的转动惯量之和。

有效质量系数：

如果计算时只取了几个振型，那么这几个振型的有效质量之和与总质量之比即为有效质量系数。

这个概念是由WILSONE.L.教授提出的，用于判断参与振型数足够与否，并将其用于ETABS程序。

振型参与质量：

某一振型的主质量（或者说该模态质量）乘以该振型的振型参与系数的平方，即为该振型的振型参与质量。

振型参与质量系数：

由于有效质量系数只实用于刚性楼板假设，现在不少结构因其复杂性需要考虑楼板的弹性变形，因此需要一种更为一般的方法，不但能够适用于刚性楼板，也应该能够适用于弹性楼板。

出于这个目的，我们从结构变形能的角度对此问题进行了研究，提出了一个通用方法来计算各地震方向的有效质量系数即振型参与质量系数，规范即是通过控制有效质量振型参与质量系数的大小来决定所取的振型数是否足够。

（见高规（5.1.13）、抗规（5.2.2）条文说明）。

这个概念不仅对糖葫芦串模型有效。

一个结构所有振型的振型参与质量之和等于各个质点的质量之和。

如果计算时只取了几个振型，那么这几个振型的振型参与质量之和与总质量之比即为振型参与质量系数。

由此可见，有效质量系数与振型参与质量系数概念不同，但都可以用来确定振型叠加法所需的振型数。

我们注意到：

ETABS6.1中，只有有效质量系数（effectivemassratio）的概念，而到了ETABS7.0以后，则出现了振型质量参与系数（modalparticipatingmassratio），可见，振型参与质量系数是有效质量系数的进一步发展，有效质量系数只适用于串连刚片系模型，分别有x方向、y方向、rz方向的有效质量系数。

振型参与质量系数则分别有x、y、z、rx、ry、rz六个方向的振型参与质量系数。

注释：

1）这里的“质量”的概念不同于通常意义上的质量。

离散结构的振型总数是有限的，振型总个数等于独立质量的总个数。

可以通过判断结构的独立质量数来了解结构的固有振型总数。

具体地说：

每块刚性楼板有三个独立质量Mx,My,Jz；

每个弹性节点有两个独立质量mx,my；

根据这两条，可以算出结构的独立质量总数，也就知道了结构的固有振型总数。

2）若记结构固有振型总数是NM，那么参与振型数最多只能选NM个，选参与振型数大于NM是错误的，因为结构没那