离散数学重点笔记文档格式.docx
《离散数学重点笔记文档格式.docx》由会员分享,可在线阅读,更多相关《离散数学重点笔记文档格式.docx(19页珍藏版)》请在冰豆网上搜索。
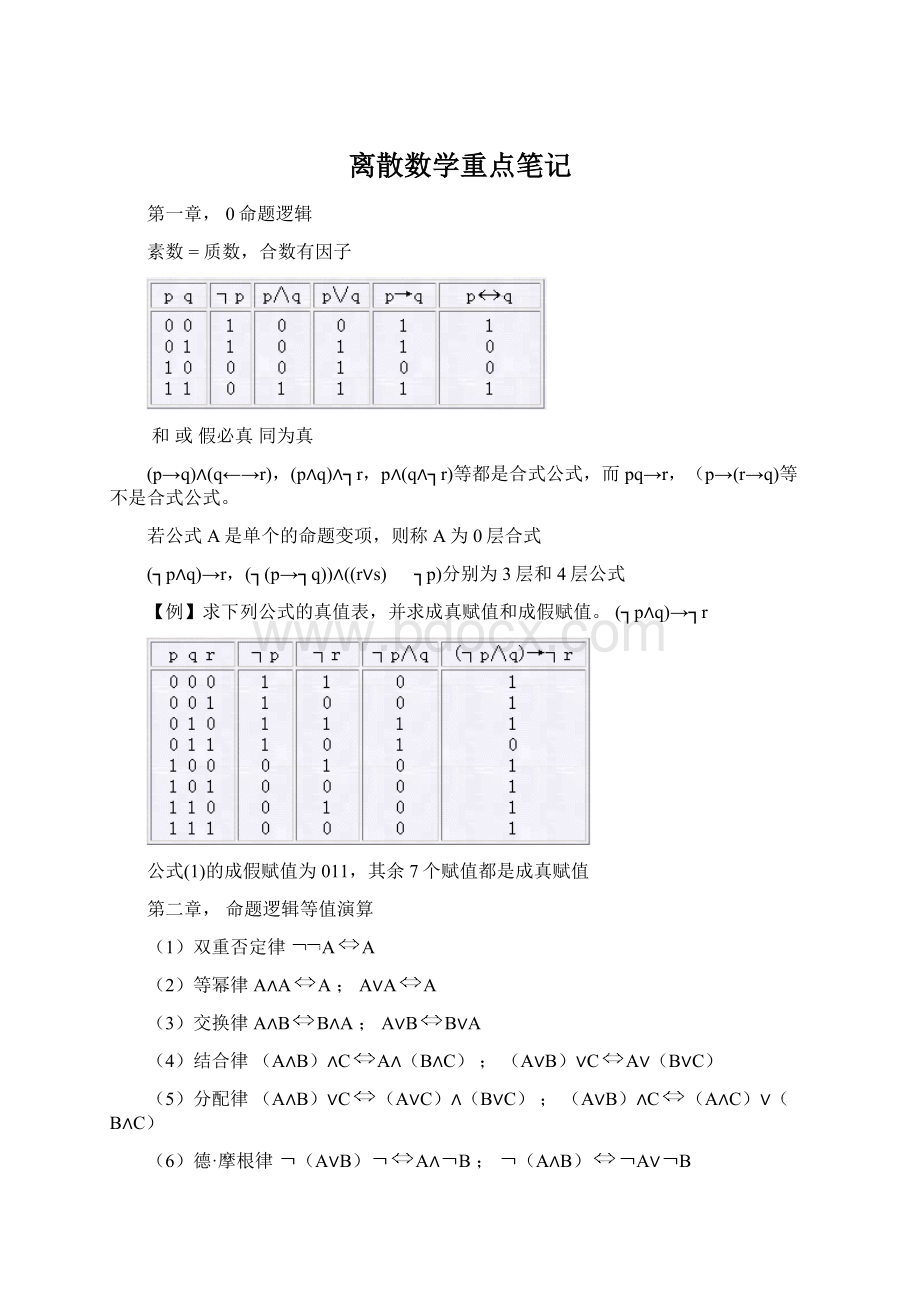
(9)同一律A∨0A;
A∧1A
(10)排中律A∨A1
(11)矛盾律A∧A0
(12)蕴涵等值式A→BA∨B
(13)假言易位A→BB→A
(14)等价等值式AB(A→B)∧(B→A)
(15)等价否定等值式ABABBA
(16)归缪式(A→B)∧(A→B)A
Ai(i=1,2,…,s)为简单合取式,则A=A1∨A2∨…∨As为析取范式(p∧┐q)∨(┐q∧┐r)∨p
A=A1∧A2∧…∧As为合取范式(p∨q∨r)∧(┐p∨┐q)∧r
一个析取范式是矛盾式当且仅当它的每个简单合取式都是矛盾式
一个合取范式是重言式当且仅当它的每个简单析取式都是重言式
主范式【∧小真,∨大假】
∧成真小写
【例】(p→q)→(┐q→┐p)
=┐(┐p∨q)∨(q∨┐p)(消去→)
=(p∧┐q)∨┐p∨q(┐内移)(已为析取范式)
=(p∧┐q)∨(┐p∧┐q)∨(┐p∧q)∨(┐p∧q)∨(p∧q)(*)
=m2∨m0∨m1∨m1∨m3
=m0∨m1∨m2∨m3(幂等律、排序)
(*)由┐p及q派生的极小项的过程如下:
┐p=┐p∧(┐q∨q)
=(┐p∧┐q)∨(┐p∧q)
q=(┐p∨p)∧q
=(┐p∧q)∨(p∧q)
熟练之后,以上过程可不写在演算过程中。
该公式中含n=2个命题变项,它的主析取范式中含了22=4个极小项,故它为重言式,
00,01,10,11全为成真赋值。
【例】
(p→q)∧┐p
=(┐p∨q)∧┐p(消去→)
=┐p∨(┐p∧q)(分配律、幂等律)已为析取范式
=m0∨m1
(p∧┐q)∨(┐p∧q)
=(p∨┐p)∧(p∨q)∧(┐q∨┐p)∧(┐q∨q)
=(p∨q)∧┐(p∧q)
重言蕴涵式
用附加前提证明法证明下面推理。
前提:
P→(Q→R),S∨P,Q结论:
S→R
证明:
(1)S∨P前提引入规则
(2)S附加前提引入规则
(3)P
(1)
(2)析取三段论规则
(4)P→(Q→R)前提引入规则
(5)Q→R(3)(4)假言推理规则
(6)Q前提引入规则
(7)R(5)(6)假言推理规则
【例】用归缪法证明。
P∨Q,P→R,Q→S结论:
S∨R
证明
(1)(S∨R)附加前提引入规则
(2)S∧R
(1)置换规则
(3)S
(2)化简规则
(4)R
(2)化简规则
(5)Q→S前提引入规则
(6)Q∨S(5)置换规则
(7)Q(3)(6)析取三段论
(8)P∨Q前提引入规则
(9)P(7)(8)析取三段论规则
(10)P→R前提引入规则
(11)P∨R(10)置换规则
(12)R(9)(11)析取三段论规则
(13)R∧R(4)(12)合取引入规则
全称量词"
"
对"
∨"
无分配律。
同样的,存在量词"
∧"
无分配律
(3)xyF(x,y)
x(F(x,a)∧F(x,b)∧F(x,c))
(F(a,a)∧F(a,b)∧F(a,c))∨(F(b,a)∧F(b,b)∧F(b,c))∨(F(c,a)∧F(c,b)∧F(c,c))
谓词逻辑的等价公式
定理1设A(x)是谓词公式,有关量词否定的两个等价公式:
(1)﹁xA(x)x﹁A(x)
(2)﹁xA(x)x﹁A(x)
定理2设A(x)是任意的含自由出现个体变项x的公式,B是不含x出现的公式,则有
(1)x(A(x)∨B)xA(x)∨B
(2)x(A(x)∧B)xA(x)∧B
(3)x(A(x)→B)xA(x)→B
(4)x(B→A(x))B→xA(x)
(5)x(A(x)∨B)xA(x)∨B
(6)x(A(x)∧B)xA(x)∧B
(7)x(A(x)→B)xA(x)→B
(8)x(B→A(x))B→xA(x)
定理3设A(x)、B(x)是任意包含自由出现个体变元x的公式,则有:
(1)x(A(x)∧B(x))xA(x)∧xB(x)
(2)x(A(x)∨B(x))xA(x)∨xB(x)
定理4下列蕴涵式成立
(1)xA(x)∨xB(x)x(A(x)∨B(x))
(2)x(A(x)∧B(x))xA(x)∧xB(x)
(3)x(A(x)→B(x))xA(x)→xB(x)
(4)x(A(x)→B(x))xA(x)→xB(x)
(5)xA(x)→xB(x)x(A(x)→B(x))
【例】在一阶逻辑自然推理系统F中构造下面推理的证明
(1)所有的人或者是吃素的或者是吃荤的,吃素的常吃豆制品,因而不吃豆制品的人是吃荤的。
(个体域为人的集合)。
(2)每个喜欢步行的人都不喜欢骑自行车,每个人或者是喜欢骑自行车或者喜欢乘汽车,有的人不喜欢乘汽车,所以有的人不喜欢步行。
【例】符号化下面的命题“所有的有理数都是实数,所有的无理数也是实数,任何虚数都不是实数,所以任何虚数既不是有理数也不是无理数”,并推证其结论。
证明设:
P(x):
x是有理数。
Q(x):
x是无理数。
R(x):
x是实数。
S(x):
x是虚数。
本题符号化为:
x(P(x)→R(x)),x(Q(x)→R(x)),
x(S(x)→﹁R(x))x(S(x)→﹁P(x)﹁R(x))
解
(1)x(S(x)→﹁R(x))P
(2)S(y)→﹁R(y)US
(1)
(3)x(P(x)→R(x))P
(4)P(y)→R(y)US(3)
(5)﹁R(y)→﹁P(y)T(4)E
(6)x(Q(x)→R(x))P
(7)Q(y)→R(y)US(6)
(8)﹁R(y)→﹁Q(y)T(7)E
(9)S(y)→﹁P(y)T
(2)(5)I
(10)S(y)→﹁Q(y)T
(2)(8)I
(11)(S(y)→﹁P(y))∧(S(y)→﹁Q(y)T(9)(10)I
(12)(﹁S(y)∨﹁P(y))∧(S(y)∨﹁Q(y))T(11)E
(13)﹁S(y)∨(﹁P(y)∧﹁Q(y))T(12)E
(14)S(y)→(﹁P(y)∧﹁Q(y))T(13)E
(15)x(S(x)→﹁P(x)∧﹁R(x))UG(14)
第六章,集合代数
自然数集合N(在离散数学中认为0也是自然数),整数集合Z,有理数集合Q,实数集合R,复数集合C
全集U,空集是一切集合的子集
(1)幂等律:
A∩A=AA∪A=A
(2)同一律:
A∩U=A
(3)零律:
A∩=A∪E=E
(4)结合律:
(A∩B)∩C=A∩(B∩C)(A∪B)∪C=A∪(B∪C)
(5)交换律:
A∩B=B∩AA∪B=B∪A
(6)分配律A∩(B∪C)=(A∩B)∪(A∩C)
A∪(B∩C)=(A∪B)∩(A∪C)
吸收律A∪(A∩B)=AA∩(A∪B)=A
同一律 A∪=A
A∩E=A
A-B称为集合B关于A的补集A-B={x|xA且xB}
补集记作~A
~(A∪B)=~A∩~B
~(A∩B)=~A∪~B
(1)双重否定律:
~(~A)=A
(2)摩根律:
~=U~U=
A-(B∪C)=(A-B)∩(A-C)
A-(B∩C)=(A-B)∪(A-C)
~(B∪C)=~B∩~C
~(B∩C)=~B∪~C
(4)矛盾律:
A∩(~A)=
(5)排中律:
A∪(~A)=U
集合A和B的对称差记作AB,它是一个集合,其元素或属于A,或属于B,但不能既属于A又属于B。
AB=(A∪B)-(A∩B)
(1)AA=
(1)
(2)A=A
(3)AU=~A
(4)AB=BA
(5)(AB)C=A(BC)
(6)AB=(A-B)∪(B-A)
第7章,二元关系
A×
B={<
x,y>
x∈A∧y∈B}
B={a,b}×
{c,d}={<
a,c>
,<
a,d>
b,c>
b,d>
}
自反性和反自反性
定义4.10设R是集合A上的二元关系,如果对于每个xA,都有<
x,x>
R,则称二元关系R是自反的。
R在A上是自反的x(xA<
R)
定义4.11设R是集合A上的二元关系,如果对于每个xA,都有<
x,x>
R,则称二元关系R是反自反的。
R在A上是反自反的x(xA<
x,x>
4.4.2对称性和反对称性
定义4.12设R是集合A上的二元关系,如果对于每个x,yA,当<
R,就有<
y,x>
R,则称二元关系R是对称的。
R在A上是对称的xy(xA∧yA∧<
R<
R)
定义4.13设R是集合A上的二元关系,如果对于每个x,yA,当<
R和<
R时,必有x=y,则称二元关系R是反对称的。
4.4.3传递性
定义4.14设R是集合A上的二元关系,如果对于任意x,y,zA,当<
R,<
y,z>
x,z>
R,则称二元关系R在A上是传递的。
R在A上是传递的xyz(xA∧yA∧zA∧<
R∧<
例4.13设A={a,b,c},R,S,T是A上的二元关系,其中
R={<
a,a>
b,b>
S={<
a,b>
c,c>
T={<
说明R,S,T是否为A上的传递关系。
解根据传递性的定义知,R和T是A上的传递关系,S不是A上的传递关系,因为
<
R,但<
R。
如果R是自反的、反对称的和传递的,则称R为A上的偏序关系,记作。
设为偏序关系,如果<
∈,则记作xy,读作“小于或等于”
【例】4、设R是二元关系,设S={<
a,b>
|存在某个c,使得<
a,c>
∈R且<
c,b>
∈R}。
证明如果R是等价关系,则S也是等价关系。
第9章,代数系统
可以用。
、*、·
、、等符号表示二元或一