空间几何体复习资料Word文档格式.doc
《空间几何体复习资料Word文档格式.doc》由会员分享,可在线阅读,更多相关《空间几何体复习资料Word文档格式.doc(9页珍藏版)》请在冰豆网上搜索。
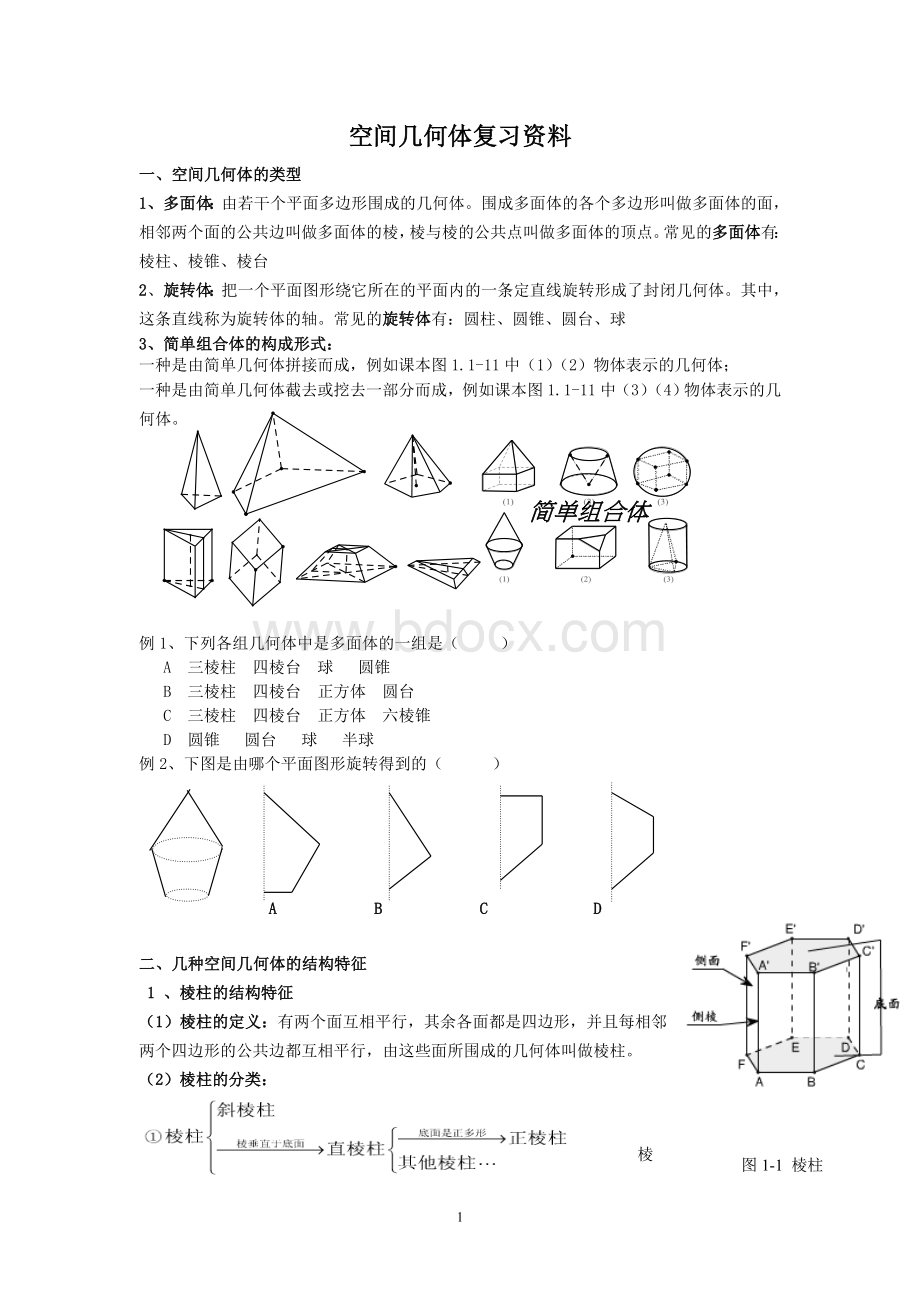
有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的几何体叫做棱柱。
(2)棱柱的分类:
图1-1棱柱
棱柱底面是四边形
四棱柱底面是平行四边形
平行六面体侧棱垂直于底面
直平行六面体底面是矩形
长方体底面是正方形
正四棱柱棱长都相等
正方体
(3)性质:
Ⅰ、侧面都是平行四边形,且各侧棱互相平行且相等;
Ⅱ、两底面是全等多边形且互相平行;
Ⅲ、平行于底面的截面和底面全等;
(4)棱柱的面积和体积公式
(是底周长,是高)
S直棱柱表面=c·
h+2S底
V棱柱=S底·
h
2、棱锥的结构特征
(1)棱锥的定义
①棱锥:
有一个面是多边形,其余各面是有一个公共顶点的三角形,由这些面所围成的几何体叫做棱锥。
②正棱锥:
如果有一个棱锥的底面是正多边形,并且顶点在底面的投影是底面的中心,这样的棱锥叫做正棱锥。
(2)正棱锥的结构特征
①平行于底面的截面是与底面相似的正多边形,相似比等于顶点到截面的距离与顶点到底面的距离之比;
它们面积的比等于截得的棱锥的高与原棱锥的高的平方比;
截得的棱锥的体积与原棱锥的体积的比等于截得的棱锥的高与原棱锥的高的立方比;
②正棱锥的各侧棱相等,各侧面是全等的等腰三角形;
A
B
C
D
P
O
H
正棱锥侧面积:
(为底周长,为斜高)
体积:
(为底面积,为高)
注:
正三棱锥是锥体中底面是等边三角形,三个侧面是全等的等腰三角形的三棱锥。
正三棱锥不等同于正四面体,正四面体必须每个面都是全等的等边三角形。
正三棱锥的性质:
1.底面是等边三角形。
2.侧面是三个全等的等腰三角形。
3.顶点在底面的射影是底面三角形的中心(也是重心、垂心、外心、内心)。
正四面体:
对于棱长为正四面体的问题可将它补成一个边长为的正方体问题。
对棱间的距离为(正方体的边长)
正四面体的高()
正四面体的体积为()
正四面体的中心到底面与顶点的距离之比为()
3、棱台的结构特征
(1)棱台的定义:
用一个平行于底面的平面去截棱锥,我们把截面和底面之间的部分称为棱台。
(2)正棱台的结构特征:
①各侧棱相等,各侧面都是全等的等腰梯形;
②正棱台的两个底面和平行于底面的截面都是正多边形;
③正棱台的对角面也是等腰梯形;
④各侧棱的延长线交于一点。
4、圆柱的结构特征
(1)圆柱的定义:
以矩形的一边所在的直线为旋转轴,其余各边旋转而形成的曲面所围成的几何体叫圆柱。
(2)圆柱的性质:
①上、下底及平行于底面的截面都是等圆;
②过轴的截面(轴截面)是全等的矩形。
(3)圆柱的侧面展开图:
圆柱的侧面展开图是以底面周长和母线长为邻边的矩形。
(4)圆柱的面积和体积公式
S圆柱侧面=2π·
r·
h(r为底面半径,h为圆柱的高)
S圆柱全=2πrh+2πr2
V圆柱=S底h=πr2h
5、圆锥的结构特征
图1-5圆锥
(1)圆锥的定义:
以直角三角形的一直角边所在的直线为旋转轴,其余各边旋转而形成的曲面所围成的几何体叫做圆锥。
(2)圆锥的结构特征:
①平行于底面的截面都是圆,截面直径与底面直径之比等于顶点到截面的距离与顶点到底面的距离之比;
②轴截面是等腰三角形;
③母线的平方等于底面半径与高的平方和:
l2=r2+h2
(3)圆锥的侧面展开图:
圆锥的侧面展开图是以顶点为圆心,以母线长为半径的扇形。
6、圆台的结构特征
(1)圆台的定义:
用一个平行于底面的平面去截圆锥,我们把截面和底面之间的部分称为圆台。
(2)圆台的结构特征:
①圆台的上下底面和平行于底面的截面都是圆;
②圆台的截面是等腰梯形;
③圆台经常补成圆锥,然后利用相似三角形进行研究。
(3)圆台的面积和体积公式
S圆台侧=π·
(R+r)·
l(r、R为上下底面半径)
S圆台全=π·
r2+π·
R2+π·
l
V圆台=1/3(πr2+πR2+πrR)h(h为圆台的高)
7、球的结构特征
(1)球的定义:
以半圆的直径所在的直线为旋转轴,半圆旋转一周形成的旋转体叫做球体。
空间中,与定点距离等于定长的点的集合叫做球面,球面所围成的几何体称为球体。
(2)球的结构特征:
①球心与截面圆心的连线垂直于截面;
②截面半径等于球半径与截面和球心的距离的平方差:
r2=R2–d2
(3)球与其他多面体的组合体的问题:
球体与其他多面体组合,包括内接和外切两种类型,解决此类问题的基本思路是:
①根据题意,确定是内接还是外切,画出立体图形;
②找出多面体与球体连接的地方,找出对球的合适的切割面,然后做出剖面图;
③将立体问题转化为平面几何中圆与多边形的问题;
④注意圆与正方体的两个关系:
球内接正方体,球直径等于正方体对角线;
球外切正方体,球直径等于正方体的边长。
(4)球的面积和体积公式:
S球面=4πR2(R为球半径)
V球=4/3πR3
结构特征
图例
棱柱
(1)两底面相互平行,其余各面都是平行四边形;
(2)侧棱平行且相等.
圆柱
(1)两底面相互平行;
(2)侧面的母线平行于圆柱的轴;
(3)是以矩形的一边所在直线为旋转轴,其余三边旋转形成的曲面所围成的几何体.
棱锥
(1)底面是多边形,各侧面均是三角形;
(2)各侧面有一个公共顶点.
圆锥
(1)底面是圆;
(2)是以直角三角形的一条直角边所在的直线为旋转轴,其余两边旋转形成的曲面所围成的几何体.
棱台
(2)是用一个平行于棱锥底面的平面去截棱锥,底面和截面之间的部分.
圆台
(2)是用一个平行于圆锥底面的平面去截圆锥,底面和截面之间的部分.
球
(1)球心到球面上各点的距离相等;
(2)是以半圆的直径所在直线为旋转轴,半圆面旋转一周形成的几何体.
例1、下列说法正确的是()
A有一个面是多边形,其余各面是三角形的多面体是棱锥
B有两个面互相平行,其余各面均为梯形的多面体是棱台
C有两个面互相平行,其余各面均为平行四边形的多面体是棱柱
D棱柱的两个底面互相平行,侧面均为平行四边形
例2、下面多面体是五面体的是()
A三棱锥B三棱柱
C四棱柱D五棱锥
例3、下列说法错误的是()
A一个三棱锥可以由一个三棱锥和一个四棱锥拼合而成
B一个圆台可以由两个圆台拼合而成
C一个圆锥可以由两个圆锥拼合而成
D一个四棱台可以由两个四棱台拼合而成
例4、下面多面体中有12条棱的是()
A四棱柱B四棱锥
C五棱锥D五棱柱
例5、在三棱锥的四个面中,直角三角形最多可有几个()
A1个B2个
C3个D4个
例6、一个棱柱有10个顶点,所有的侧棱长的和为60cm,则每条侧棱长为___________cm.
三、空间几何体的表面积和体积
1、空间几何体的表面积:
棱柱、棱锥的表面积:
各个面面积之和
圆柱的表面积:
圆锥的表面积:
圆台的表面积:
球的表面积:
扇形的面积公式(其中表示弧长,表示半径,表示弧度)
2、空间几何体的体积:
柱体的体积:
锥体的体积:
台体的体积:
球体的体积:
例1、一个圆柱的侧面展开图是一个正方形,这个圆柱的全面积与侧面积的比是()
AB
CD
例2、已知圆锥的母线长为8,底面圆周长为,则它的体积是()
AB9
例3、若圆台的上下底面半径分别是1和3,它的侧面积是两底面面积的2倍,则圆台的母线长是()
A2B2.5
C5D10
A
A1
B1
C1
D1
例4、若圆锥的侧面展开图是圆心角为1200,半径为的扇形,则这个圆锥的表面积与侧面积的比是()
A3:
2B2:
1
C4:
3D5:
3
例5、如图,在棱长为4的正方体ABCD-A1B1C1D1中,P是A1B1上一点,
且PB1=A1B1,则多面体P-BCC1B1的体积为()
ABC4D16
例6、两个平行于圆锥底面的平面将圆锥的高分成相等的三部分,则圆锥被分成的三部分的体积的比是()
A1:
2:
3B1:
7:
19
C3:
4:
5D1:
9:
27
例7、如图,一个三棱锥,底面ABC为正三角形,侧棱SA=SB=SC=1,,M、N分别为棱SB和SC上的点,求的周长的最小值。
M
S
N
四、空间几何体的三视图和直观图
1、三视图:
把光由一点向外散射形成的投影叫中心投影,中心投影的投影线交于一点;
把在一束平行光线照射下的投影