北京高考真题数学理含解析Word文档格式.docx
《北京高考真题数学理含解析Word文档格式.docx》由会员分享,可在线阅读,更多相关《北京高考真题数学理含解析Word文档格式.docx(17页珍藏版)》请在冰豆网上搜索。
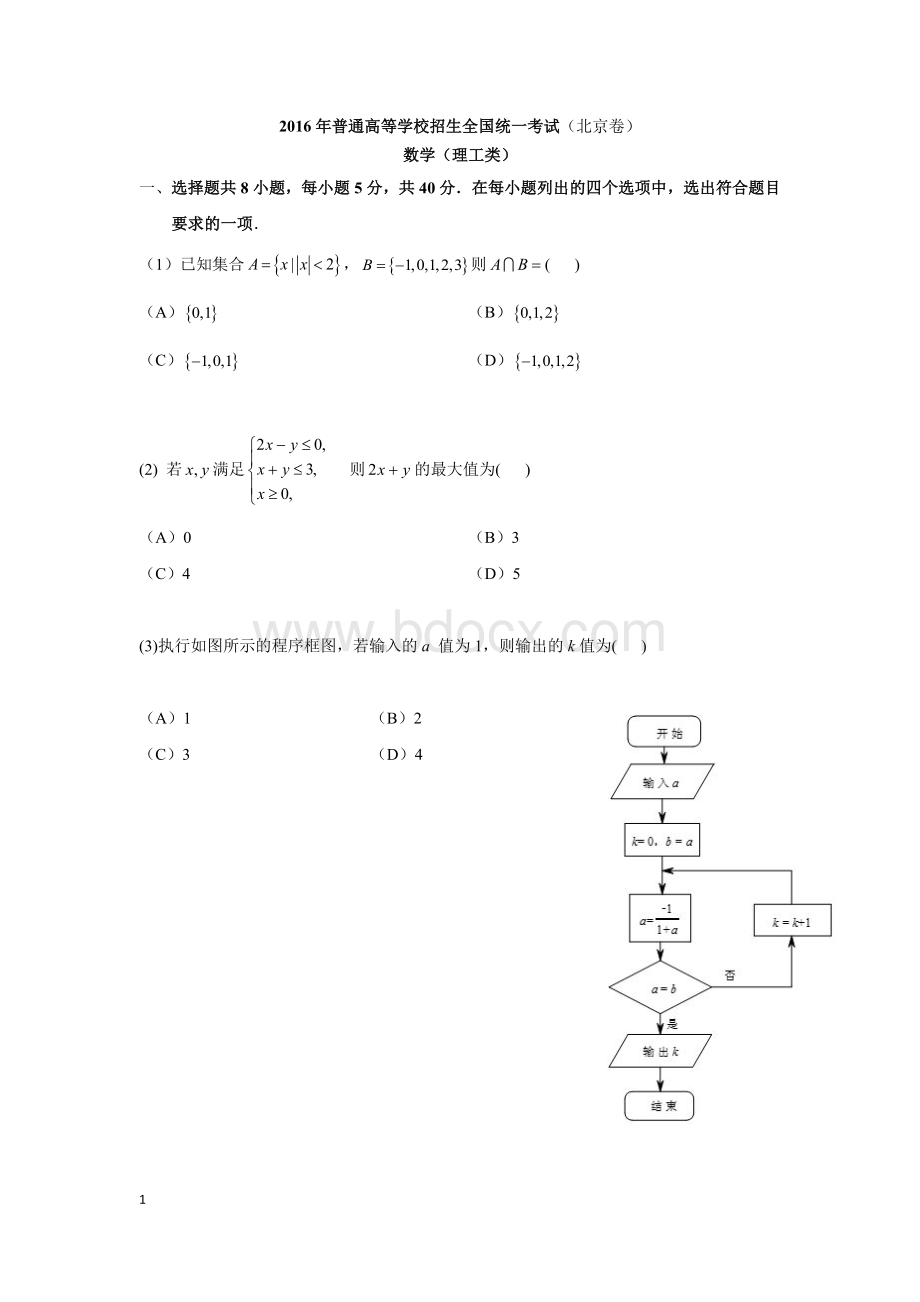
(A)充分而不必要条件(B)必要而不充分条件
(C)充分必要条件(D)既不充分也不必要条件
(5)已知,且,则()
(A)(B)(C)(D)
(6)某三棱锥的三视图如图所示,则三棱锥的体积为()
(7)将函数图像上的点向左平移个单位长度得到点.若位于函数的图像上,则()
(A),的最小值为(B),的最小值为
(C),的最小值为(D),的最小值为
(8)袋中装有偶数个球,其中红球,黑球各占一半,甲,乙,丙是三个空盒,每次从袋中随意取出两个球,将期中一个球放入甲盒,如果这个球是红球,就将另一个球放入乙盒,否则放入丙盒,重复上述过程,直到袋中所有球都被放入盒中,则().
(A)乙盒中黑球不多于丙盒中黑球(B)乙盒中红球与丙盒中黑球一样多
(C)乙盒中的红球不多于丙盒中红球(D)乙盒中黑球与丙盒中红球一样多
二、填空题共6题,每小题5分,共30分.
(9)设,若复数在复平面内对应的点位于实轴上,则__________.
(10)在的展开式中,的系数为__________.
(11)在极坐标系中,直线与圆交于两点,则__________.
(12)已知为等差数列,为其前项和.若,则__________.
(13)双曲线的渐近线为正方形的边所在的直线,点为该双曲线的焦点,若正方形的边长为,则__________.
(14)设函数
①若,则的最大值__________.
②若无最大值,则实数的取值范围是__________.
三、解答题:
本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程.
15.(本小题13分)在中,
(1)求的大小.
(2)求的最大值.
16.(本小题13分),,三班共有名学生,为调查他们的体育锻炼情况,通过分层抽样获得了部分学生一周的锻炼时间,数据如下表(单位:
小时);
(Ⅰ)试估计班的学生人数;
(Ⅱ)从班和班抽出的学生中,各随机选取一人,班选出的人记为甲,班选出的人记为乙,假设所有学生的锻炼时间相互独立,求该周甲的锻炼时间比乙的锻炼时间长的概率;
(Ⅲ)再从,,三班中个随机抽取抽取一名学生,题目该周期的锻炼时间分别是,,(单位:
小时),这个新数据与表格构成的新样本的平均数记为,表格中的数据的平均数记为,试判断和的大小.(结论不要求证明)
17.(本小题14分)如图,在四棱锥中,平面平面,,,,
,,.
(Ⅰ)求证:
平面;
(Ⅱ)求直线与平面所成角的正弦值;
(Ⅲ)在棱上是否存在点,使得平面?
若存在,求的值;
若不存在,说明理由.
(18)(本小题13分)
设函数,曲线在点处的切线方程为.
(1)求的值;
(2)求的单调区间.
(19)(本小题14分)
已知椭圆的离心率为,,,,的面积为.
(1)求椭圆的方程;
(2)设是椭圆上的一点,直线与轴交于点,直线与轴交于点,求证:
为定值.
20.(本小题13分)设数列如果对小于的每一个正整数都有则称是数列的一个”时刻”.记是数列的所有”时刻”组成的集合.
对数列写出的所有元素;
证明:
若数列中存在使得,则;
若数列满足,则的元素个数不小于.
数学答案(理工类)
一、选择题
(1)解析,集合所以选c
(2)解析如图当取点A(1,2)时,取到最大值4
选C
(3)循环一次,,,;
循环二次,,;
循环三次,,,
故答案选B.
4.当与方向相反时,不能得到;
而当时,平方得,即,因此与可以不相等,
因此选既不充分也不必要.
选D
5.【答案】C
【解析】特殊值法:
A取排除,B取排除,D取排除,C由单调性可知移项正确.
(6)A
【解析】三视图还原如右图所示:
则三棱锥的体积
7.【答案】A
【解析】点在函数上,所以,
即,根据平移的原则,有,
根据题意有,结合余弦函数的图像可知满足余弦值等于的最小正角为,故的最小值为.
(8)共两个球时有以下两种情况
甲乙丙
红黑
黑
红
可排除A和D
四个球时的其中一种情况如下
红红
黑
可排除C
故:
答案选B
分析:
此题重点考察了选择题的一个重要做题思想:
特值法、排除法.此外,还考察了学生的逻辑思维能力,以及在紧急状态下的应变能力.
(9)设,若复数在复平面内对应的点位于实轴上,则___.
解答:
,因为复数在实轴上,所以有.
答案:
(10)在的展开式中,的系数为___.
其中含有的项为,所以的系数为
60
(11)在极坐标系中,直线与圆交于两点,则___.
解:
,所以可以变形为,可以变形为.因为直线过点,圆的圆心也是,所以交线为直径,又因为,所以
2
(12)已知为等差数列,为其前项和.若,则___.
为等差数列,,所以,解得.所以
6
(13)双曲线的渐近线为正方形的边所在的直线,点为该双曲线的焦点,若正方形的边长为,则___.
因为两条渐近线是正方形的相邻两边,所以夹角为,可知渐近线的斜率为,所以.因为为该双曲线的焦点,所以,由可得.
①若,则的最大值___.
②若无最大值,则实数的取值范围是___.
①当时,函数变为.当时,,在单增,在单减.所以时,的最大值是;
时,单减,,所以若,则的最大值为.
②函数的最大值只会在三个位置取到——极大值点、端点以及断点.,因为,在单增,存在最大值为,所以,当时,,在上,,所以很有最大值为.而题目要求不存在最大值,所以是无法取到的,所以.
2,
三、解答题
15.在中,
(3)求的大小.
(4)求的最大值.
(1),,,
(2)在中,,
,所以当时,的最大值为.
16.,,三班共有名学生,为调查他们的体育锻炼情况,通过分层抽样获得了部分学生一周的锻炼时间,数据如下表(单位:
解析:
(Ⅰ)设班的学生人数为,
则,解得;
(Ⅱ)记该周甲的锻炼时间比乙的锻炼时间长为事件;
由题可知,从班和班抽出的学生中,各随机选取一人,共有种;
满足条件的有,,,,,,,,
,,,,,,共种;
所以,;
(Ⅲ).
(提示:
新选出,,的平均数约为;
,,的三组数据均为等差数列,平均数分别为,,,整体平均数显然大于)
17.如图,在四棱锥中,平面平面,,,,
(Ⅰ)证明:
面面,
面面,
∵,面,
∴面,
∵面,
∴,又,
面;
(Ⅱ)取的中点,连结,,
∵,∴,
以为原点,建立如图坐标系;
易知,,,,
则,,,,
设平面的法向量为,
则,解得,
设直线与平面所成角为,
;
(Ⅲ)假设存在,使得平面,设,
,,
,得,
,
∵平面,平面的法向量为,
∴,即,解得,
即当时,满足题意.
18.
(1)解析:
,根据题意,有
.
(2)解析:
由
(1),,导函数分母为正,只需考虑分子的符号即可.
构造函数,.
故在上单调递减,在上单调递增,
,即恒成立且不恒为,因此且不恒为.
故在上单调递增,无单调递减区间.
19.【解析】
(1)由题意得,,,又因为解得,,,故方程为
(2)当在左顶点处时,所以,当在下顶点时,,当在上顶点时,不合题意,当不在顶点处,设,则,即,
又因为,,则直线:
,令,得
直线:
,,
20.解:
(I)的所有元素:
(II)证明:
不妨设中的最大值第一次出现时为,
则由可得
因此对小于的每个正整数都有,
故,所以;
(III)证明:
①当时,显然成立;
②当时,先证明数列中第一次出现比大的数应属于区间,否则假设第一次出现比大的数为,则,矛盾,故结论成立.
依题
同理数列中第一次出现比大的数时应属于区间,其对应的项也都是数列的“时刻”
若,则至少对应个“时刻”;
若,则第一次出现比大的数时所对应的项数也为数列的“时刻”,则至少会有个“时刻”;
综上,的元素个数不小于
17