最新版人教版七年级数学全册知识点Word文件下载.docx

最新版人教版七年级数学全册知识点Word文件下载.docx

《最新版人教版七年级数学全册知识点Word文件下载.docx》由会员分享，可在线阅读，更多相关《最新版人教版七年级数学全册知识点Word文件下载.docx（15页珍藏版）》请在冰豆网上搜索。

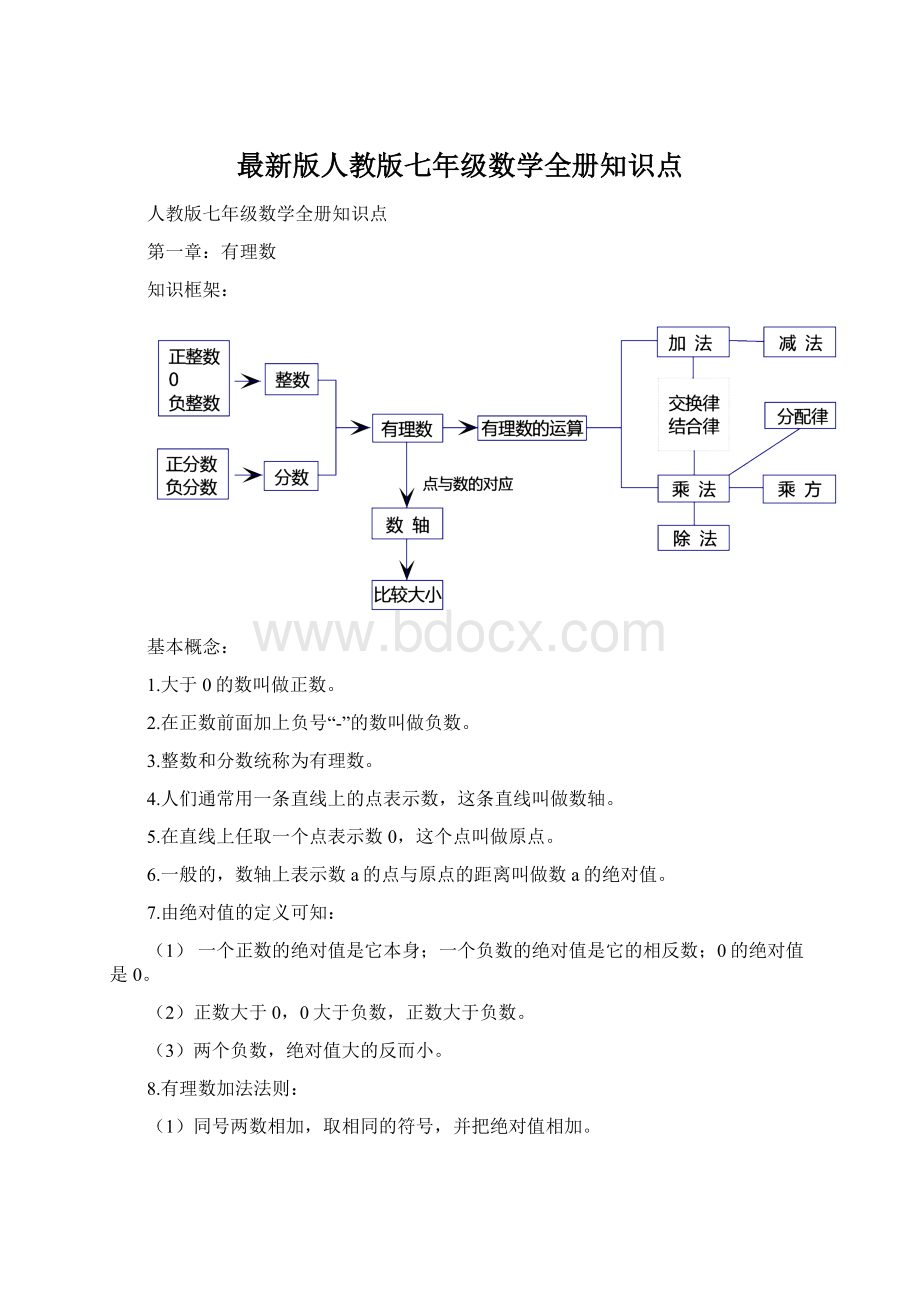
减去一个数，等于加上这个数的相反数。

12.有理数乘法法则

两数相乘，同号得正，异号得负，并把绝对值向乘。

任何数同0相乘，都得0。

13.有理数中仍然有：

乘积是1的两个数互为倒数。

14.一般的，有理数乘法中，两个数相乘，交换因数的位置，积相等。

三个数相乘，先把前两个数相乘，或者先把后两个数相乘，积相等。

15.一般地，一个数同两个数的和相乘，等于把这个数分别同这两个数相乘，再把积相加。

16.有理数除法法则

除以一个不等于0的数，等于乘这个数的倒数。

两数相除，同号得正，异号得负，并把绝对值相除。

0除以任何一个不等于0的数，都得0。

17.求n个相同因数的积的运算，叫做乘方，乘方的结果叫做幂。

在an中，a叫做底数，n叫做指数

18.根据有理数的乘法法则可以得出

负数的奇次幂是负数，负数的偶次幂是正数。

显然，正数的任何次幂都是正数，0的任何次幂都是0。

19.做有理数混合运算时，应注意以下运算顺序：

先乘方，再乘除，最后加减；

同级运算，从左到右进行；

如有括号，先做括号内的运算，按小括号、中括号、大括号依次进行。

20.把一个大于10数表示成a×

10n的形式（其中a是整数数位只有一位的数，n是正整数），使用的是科学计数法。

21.接近实际数字，但是与实际数字还是有差别，这个数是一个近似数。

22.从一个数的左边的第一个非0数字起，到末尾数字止，所有的数字都是这个数的有效数字。

二:

整式的加减

1.都是数或字母的积的式子叫做单项式，单独的一个数或一个字母也是单项式。

2.单项式中的数字因数叫做这个单项式的系数。

3.一个单项式中，所有字母的指数的和叫做这个单项式的次数。

4.几个单项的和叫做多项式，其中，每个单项式叫做多项式的项，不含字母的项叫做常数项

5.多项式里次数最高项的次数，叫做这个多项式的次数。

6.把多项式中的同类项合并成一项，叫做合并同类项。

合并同类项后，所得项的系数是合并前各同类项的系数的和，且字母部分不变。

如果括号外的因数是正数，去括号后原括号内各项的符号与原来的符号相同；

如果括号外的因数是负数，去括号后原括号内各项的符号与原来的符号相反。

一般地，几个整式相加减，如果有括号就先去括号，然后再合并同类项。

三:

一元一次方程

1.列方程时，要先设字母表示未知数，然后根据问题中的相等关系，写出还有未知数的等式——方程。

2.含有一个未知数（元），未知数的次数都是1，这样的方程叫做一元一次方程。

3.分析实际问题中的数量关系，利用其中的等量关系列出方程，是用数学解决实际问题的一种方法。

4.等式的性质1：

等式两边加（或减）同一个数（或式子），结果仍相等。

5.等式的性质2：

等式两边乘同一个数，或除以一个不为0的数，结果仍相等。

6.把等式一边的某项变号后移到另一边，叫做移项。

7.应用：

行程问题：

s=v×

t工程问题：

工作总量=工作效率×

时间

盈亏问题：

利润=售价－成本利率=利润÷

成本×

100％

售价=标价×

折扣数×

10％

储蓄利润问题：

利息=本金×

利率×

时间本息和=本金+利息

四:

图形初步认识

1.我们把实物中抽象的各种图形统称为几何图形。

2.有些几何图形（如长方体、正方体、圆柱、圆锥、球等）的各部分不都在同一平面内，它们是立体图形。

3.有些几何图形（如线段、角、三角形、长方形、圆等）的各部分都在同一平面内，它们是平面图形。

4.将由平面图形围成的立体图形表面适当剪开，可以展开成平面图形，这样的平面图形称为相应立体图形的展开图。

5.几何体简称为体。

6.包围着体的是面，面有平的面和曲的面两种。

7.面与面相交的地方形成线，线和线相交的地方是点。

8.点动成面，面动成线，线动成体。

9.经过探究可以得到一个基本事实：

经过两点有一条直线，并且只有一条直线。

简述为：

两点确定一条直线（公理）。

10.当两条不同的直线有一个公共点时，我们就称这两条直线相交，这个公共点叫做它们的交点。

11.点M把线段AB分成相等的两条线段AM和MB，点M叫做线段AB的中点。

12.经过比较，我们可以得到一个关于线段的基本事实：

两点的所有连线中，线段最短。

简单说成：

两点之间，线段最短。

（公理）

13.连接两点间的线段的长度，叫做这两点的距离。

14.角∠也是一种基本的几何图形。

15.把一个周角360等分，每一份就是1度的角，记作1°

；

把一度的角60等分，每一份叫做1分的角，记作1′；

把1分的角60等分，每一份叫做1秒的角，记作1″。

16.从一个角的顶点出发，把这个角分成相等的两个角的射线，叫做这个角的平分线。

17.如果两个角的和等于90°

（直角），就是说这两个叫互为余角，即其中的每一个角是另一个角的余角。

18.如果两个角的和等于180°

（平角），就说这两个角互为补角，即其中一个角是另一个角的补角

19.等角的补角相等，等角的余角相等。

第五章　相交线与平行线

一、知识网络结构

二、知识要点

1、在同一平面内，两条直线的位置关系有两种：

相交和平行，垂直是相交的一种特殊情况。

2、在同一平面内，不相交的两条直线叫平行线。

如果两条直线只有一个公共点，称这两条直线相交；

如果两条直线没有公共点，称这两条直线平行。

3、两条直线相交所构成的四个角中，有公共顶点且有一条公共边的两个角是

邻补角。

邻补角的性质：

邻补角互补。

如图1所示，∠1与∠2互为邻补角，∠2与∠3互为邻补角，∠3与∠4互为邻补角，∠4与∠1互为邻补角。

∠1+∠2=180°

∠2+∠3=180°

∠3+∠4=180°

∠4+∠1=180°

。

4、两条直线相交所构成的四个角中，一个角的两边分别是另一个角的两边的反向延长线，这样的两个角互为对顶角。

对顶角的性质：

对顶角相等。

如图1所示，∠1与∠3互为对顶角，∠1与∠3互为对顶角。

∠1=∠3；

∠2=∠4。

5、两条直线相交所成的角中，如果有一个是直角或90°

时，称这两条直线互相垂直，

其中一条叫做另一条的垂线。

如图2所示，当∠1或∠2或∠3或∠4=90°

时，a⊥b。

垂线的性质：

性质1：

过一点有且只有一条直线与已知直线垂直。

性质2：

连接直线外一点与直线上各点的所有线段中，垂线段最短。

性质3：

如图2所示，当a⊥b时，∠1=∠2=∠3=∠4=90°

点到直线的距离：

直线外一点到这条直线的垂线段的长度叫点到直线的距离。

6、同位角、内错角、同旁内角基本特征：

①在两条直线（被截线）的同一方，都在第三条直线（截线）的同一侧，这样

的两个角叫同位角。

图3中，共有4对同位角：

∠1与∠5是同位角；

∠2与∠6是同位角；

∠3与∠7是同位角；

∠4与∠8是同位角。

②在两条直线（被截线）之间，并且在第三条直线（截线）的两侧，这样的两个角叫内错角。

图3中，共有2对内错角：

∠1与∠7是内错角；

∠4与∠6是内错角。

③在两条直线（被截线）的之间，都在第三条直线（截线）的同一旁，这样的两个角叫同旁内角。

图3中，共有2对同旁内角：

∠1与∠6是同旁内角；

∠4与∠7是同旁内角。

7、平行公理：

经过直线外一点有且只有一条直线与已知直线平行。

平行公理的推论：

如果两条直线都与第三条直线平行，那么这两条直线也互相平行。

平行线的性质：

两直线平行，同位角相等。

如图4所示，如果a∥b，

两直线平行，内错角相等。

如图4所示，如果a∥b，则∠1=∠7；

∠4=∠6。

两直线平行，同旁内角互补。

如图4所示，如果a∥b，则∠1+∠6=180°

∠4+∠7=180°

性质4：

平行于同一条直线的两条直线互相平行。

如果a∥b，a∥c，则b∥c。

8、平行线的判定：

判定1：

同位角相等，两直线平行。

如图5所示，如果∠1=∠5或∠2=∠6或∠3=∠7或

∠4=∠8，则a∥b。

判定2：

内错角相等，两直线平行。

如图5所示，如果∠1=∠7或∠4=∠6，则a∥b。

判定3：

同旁内角互补，两直线平行。

如图5所示，如果∠1+∠6=180°

或∠4+∠7=180°

，则a∥b。

判定4：

9、判断一件事情的语句叫命题。

命题由题设和结论两部分组成，有真命题和假命题之分。

如果题设成立，那么结论一定成立，这样的命题叫真命题；

如果题设成立，那么结论不一定成立，这样的命题叫假命题。

真命题的正确性是经过推理证实的，这样的真命题叫定理，它可以作为继续推理的依据。

10、平移：

在平面内，将一个图形沿某个方向移动一定的距离，图形的这种移动叫做平移变换，简称平移。

平移后，新图形与原图形的形状和大小完全相同，改变的是图形的位置。

平移后得到的新图形中每一点，都是由原图形中的某一点移动后得到的，这样的两个点叫做对应点。

平移性质：

平移前后两个图形中①对应点的连线段平行且相等；

②对应线段相等；

③对应角相等。

第六章　实数

【知识点一】实数的分类

1、按定义分类：

正有理数

有理数零有限小数和无限循环小数

实数负有理数

正无理数

无理数无限不循环小数

负无理数

2、按性质符号分类：

正实数

实数0正无理数

负有理数

负实数负无理数

注：

0既不是正数也不是负数.

【知识点二】实数的相关概念

1.相反数

（1）代数意义：

只有符号不同的两个数，我们说其中一个是另一个的相反数。

0的相反数是0。

（2）几何意义：

在数轴上原点的两侧，与原点距离相等的两个点表示的两个数互为相反数，或数轴上，互为相反数的两个数所对应的点关于原点对称。

（3）互为相反数的两个数之和等于0。

若a、b互为相反数，则a+b=0。

2.绝对值 

|a|≥0。

正数的绝对值等于它本身，负数的绝对值等于它的相反数，0的绝对值等于0。

3.倒数

（1）0没有倒数 

（2）乘积是1的两个数互为倒数。

若a、b互为倒数则ab=1。

4.平方根

（1）如果一个数的平方等于a，这个数就叫做a的平方根．一个正数有两个平方根，它们互为相反数；

0有一个平方根，它是0本身；

负数没有平方根．a（a≥0）的平方根记作。

（2）一个正数a的正的平方根，叫做a的算术平方根。

0的算术平方根是0。