上海市2013年春沪教版数学八年级下册《四边形》练习题(有答案)Word文件下载.doc
《上海市2013年春沪教版数学八年级下册《四边形》练习题(有答案)Word文件下载.doc》由会员分享,可在线阅读,更多相关《上海市2013年春沪教版数学八年级下册《四边形》练习题(有答案)Word文件下载.doc(15页珍藏版)》请在冰豆网上搜索。
四边形是平行四边形;
(2)联结,若平分,
四边形是矩形.
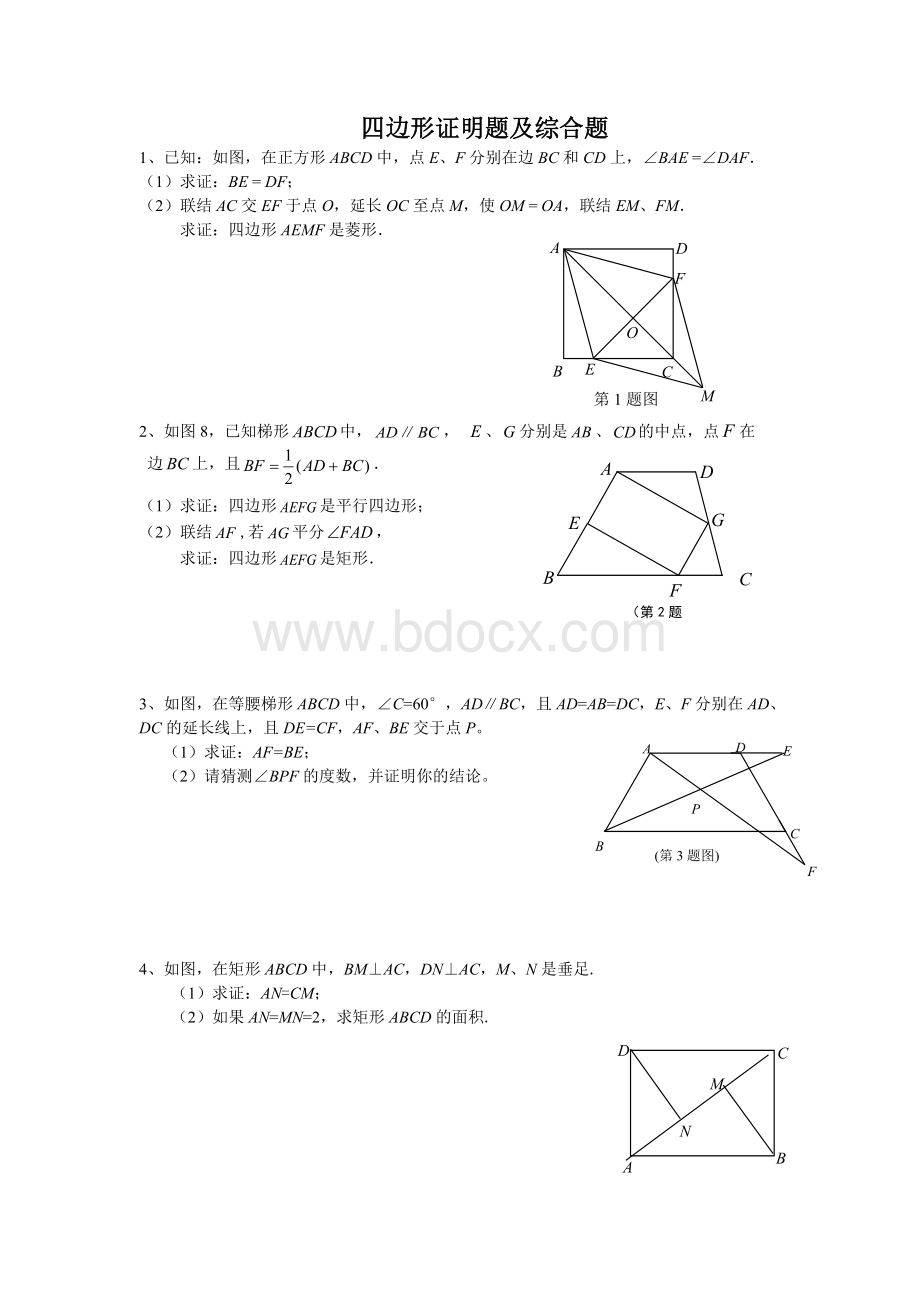
(第3题图)
P
3、如图,在等腰梯形ABCD中,∠C=60°
,AD∥BC,且AD=AB=DC,E、F分别在AD、DC的延长线上,且DE=CF,AF、BE交于点P。
AF=BE;
(2)请猜测∠BPF的度数,并证明你的结论。
4、如图,在矩形ABCD中,BM⊥AC,DN⊥AC,M、N是垂足.
N
AN=CM;
(2)如果AN=MN=2,求矩形ABCD的面积.
(图5)
5.如图.在平行四边形中,为对角线的交点,点为线段延长线上的一点,且.过点作∥,交于点,联结.
∥;
(2)如果梯形是等腰梯形,判断四边形的形状,
并给出证明.
(第6题)
G
H
6、如图,在正方形ABCD中,点E、F分别是边AB、AD的中点,DE与CF相交于G,DE、CB的延长线相交于点H,点M是CG的中点.
求证:
(1)BM//GH;
(2)BM⊥CF.
7.已知:
如图,AE∥BF,AC平分∠BAD,交BF于点C,BD平分∠ABC,交AE于点D,联结CD.求证:
四边形ABCD是菱形.
8.如图,在正方形中,点、分别是边、的中点,与相交于,、的延长线相交于点,点是的中点.
(1)
(2)
9.已知:
如图,在梯形ABCD中,AD//BC,AB=CD,点E、F在边BC上,BE=CF,EF=AD.
四边形AEFD是矩形.
(第9题)
10.如图,在□ABCD中,E、F分别为边ABCD的中点,BD是对角线,过A点作AG//DB交CB的延长线于点G.
DE∥BF;
(2)若∠G=,求证:
四边形DEBF是菱形.
11.(第11题图)
已知:
如图,在梯形ABCD中,AD//BC,BC=2AD,AC⊥AB,点E是AC的中点,DE的延长线与边BC相交于点F.
四边形AFCD是菱形.
12.(本题共2小题,每小题6分,满分12分)
(第12题图)
如图,在梯形ABCD中,AD//BC,点E、F在边BC上,DE//AB,AF//CD,且四边形AEFD是平行四边形.
(1)试判断线段AD与BC的长度之间有怎样的数量关系?
并证明你的结论;
(2)现有三个论断:
①AD=AB;
②∠B+∠C
=90°
;
③∠B=2∠C.请从上述三个论断中选择一个论断作为条件,证明四边形AEFD是菱形.
13.已知:
如图,矩形纸片ABCD的边AD=3,CD=2,点P是边CD上的一个动点(不与点C重合,把这张矩形纸片折叠,使点B落在点P的位置上,折痕交边AD与点M,折痕交边BC于点N.
(1)写出图中的全等三角形.设CP=,AM=,写出与的函数关系式;
(2)试判断∠BMP是否可能等于90°
.如果可能,请求出此时CP的长;
如果不可能,请说明理由.
14、已知边长为1的正方形ABCD中,P是对角线AC上的一个动点(与点A、C不重合),
过点P作PE⊥PB,PE交射线DC于点E,过点E作EF⊥AC,垂足为点F.
(1)当点E落在线段CD上时(如图10),
①求证:
PB=PE;
②在点P的运动过程中,PF的长度是否发生变化?
若不变,试求出这个不变的值,
若变化,试说明理由;
(2)当点E落在线段DC的延长线上时,在备用图上画出符合要求的大致图形,并判断
上述
(1)中的结论是否仍然成立(只需写出结论,不需要证明);
(3)在点P的运动过程中,⊿PEC能否为等腰三角形?
如果能,试求出AP的长,如果
不能,试说明理由.
。
(图1)
(备用图)
15、如图,直线与轴相交于点,与直线相交于点.
(1)求点的坐标.
(2)请判断△的形状并说明理由.
(3)动点从原点出发,以每秒1个单位的速度沿着的路线向点匀速运动(不与点、重合),过点分别作轴于,轴于.设运动秒时,矩形与△重叠部分的面积为.求与之间的函数关系式.
16.已知:
如图,梯形中,∥,,,.是直线上一点,联结,过点作交直线于点.联结.
(1)若点是线段上一点(与点、不重合),(如图1所示)
①求证:
.
②设,△的面积为,求关于的函数解析式,并写出此函数的定义域.
(第3题图1)
(2)直线上是否存在一点,使△是△面积的3倍,若存在,直接写出的长,若不存在,请说明理由.
(第3题备用图)
17.已知:
O为正方形ABCD对角线的交点,点E在边CB的延长线上,联结EO,OF⊥OE交BA延长线于点F,联结EF(如图4)。
(1)求证:
EO=FO;
(2)若正方形的边长为2,OE=2OA,求BE的长;
(3)当OE=2OA时,将△FOE绕点O逆时针旋转到△F1OE1,使得∠BOE1=时,试猜想并证明△AOE1是什么三角形。
(图4)
18.(本题满分10分,第
(1)小题3分,第
(2)小题4分,第(3)小题3分)
如图,在正方形ABCD中,点E、F分别在BC、AD的延长线上,且EA⊥CF,垂足为H,
AE与CD相交于点G.
AG=CF;
(2)当点G为CD的中点时(如图1),求证:
FC=FE;
(3)如果正方形ABCD的边长为2,当EF=EC时(如图2),求DG的长.
图2
图1
答案
1.证明:
(1)∵正方形ABCD,∴AB=AD,∠B=∠D=90°
…………………………(2分)
∵∠BAE=∠DAF
∴△ABE≌△ADF……………………………………………………………(1分)
∴BE=DF……………………………………………………………………(2分)
(2)∵正方形ABCD,∴∠BAC=∠DAC………………………………………(1分)
∵∠BAE=∠DAF∴∠EAO=∠FAO……………………………………(1分)
∵△ABE≌△ADF∴AE=AF…………………………………………(1分)
∴EO=FO,AO⊥EF…………………………………………………………(2分)
∵OM=OA∴四边形AEMF是平行四边形……………………………(1分)
∵AO⊥EF∴四边形AEMF是菱形……………………………………(1分)
2.
(1)证明:
联结EG,
∵梯形中,,且、分别是、的中点,
∴EG//BC,且,…………………………(2分)
又∵
∴EG=BF.……………………………………………………(1分)
∴四边形是平行四边形.…………………(2分)
(2)证明:
设AF与EG交于点O,
∵EG//AD,∴∠DAG=∠AGE
∵平分,∴∠DAG=∠GAO
∴∠GAO=∠AGE
∴AO=GO.………………………………(2分)
∵四边形是平行四边形,
∴AF=EG,四边形是矩形…………………………(2分)
3.证明:
(1)∵梯形ABCD是等腰梯形,AD∥BC
∴∠BAE=∠ADF………………………………………………(1分)
∵AD=DC∴AE=DF…………………………………………(1分)
∵BA=AD∴△BAE≌△ADF,…………………………………(1分)
∴BE=AF.…………………………………………………………(1分)
(2)猜想∠BPF=120°
.……………………………………………………(1分)
∵由
(1)知△BAE≌△ADF,∴∠ABE=∠DAF.…………………(1分)
∴∠BPF=∠ABE+∠BAP=∠BAE.……………………………………(1分)
而AD∥BC,∠C=∠ABC=60°
,∴=120°
∴∠BPF=∠BAE=120°
.………………………………………………(1分)
4、证:
(1)∵四边形ABCD是矩形,
∴AD∥BC,AD=BC.
∴∠DAC=∠BCA.
又∵DN⊥AC,BM⊥AC,
∴∠DNA=∠BMC.
∴⊿DAN≌⊿BCM,---------------------------------------------------(3分)
∴AN=CM.---------------------------------------------------------------(1分)
(2)联结BD交AC于点O,
∵AN=NM=2,
∴AC=BD=6,
又∵四边形ABCD是矩形,
∴AO=DO=3,
在⊿ODN中,OD=3,ON=1,∠OND=,
∴DN=,--------------------------------------(2分)
∴矩形ABCD的面积=.-----------------------(1分)
(第5题图1)
5.解:
(1)方法1:
延长交于(如图1).……………1分
在平行四边形中,∥,.
∵∥,∥,
∴四边形是平行四边形.
∴.……………1分
又∵,,
∵∥,∴.
在和中,
∵,,,
∴≌(A.A.S).∴.…………………1分
∵四边形是平行四边形,∴.
∴∥.………………1分
(第5题图2)
方法2:
将线段的中点记为,联结(如图2).………………1分
∴∥.…………1分
∴.
∵,,
∴≌(A.S.A).…………………1分
又∵∥,
∴四边形是平行四边形.…………………1分
∴∥.…………………1分