全等三角形提高题含答案Word格式文档下载.docx

全等三角形提高题含答案Word格式文档下载.docx

《全等三角形提高题含答案Word格式文档下载.docx》由会员分享，可在线阅读，更多相关《全等三角形提高题含答案Word格式文档下载.docx（13页珍藏版）》请在冰豆网上搜索。

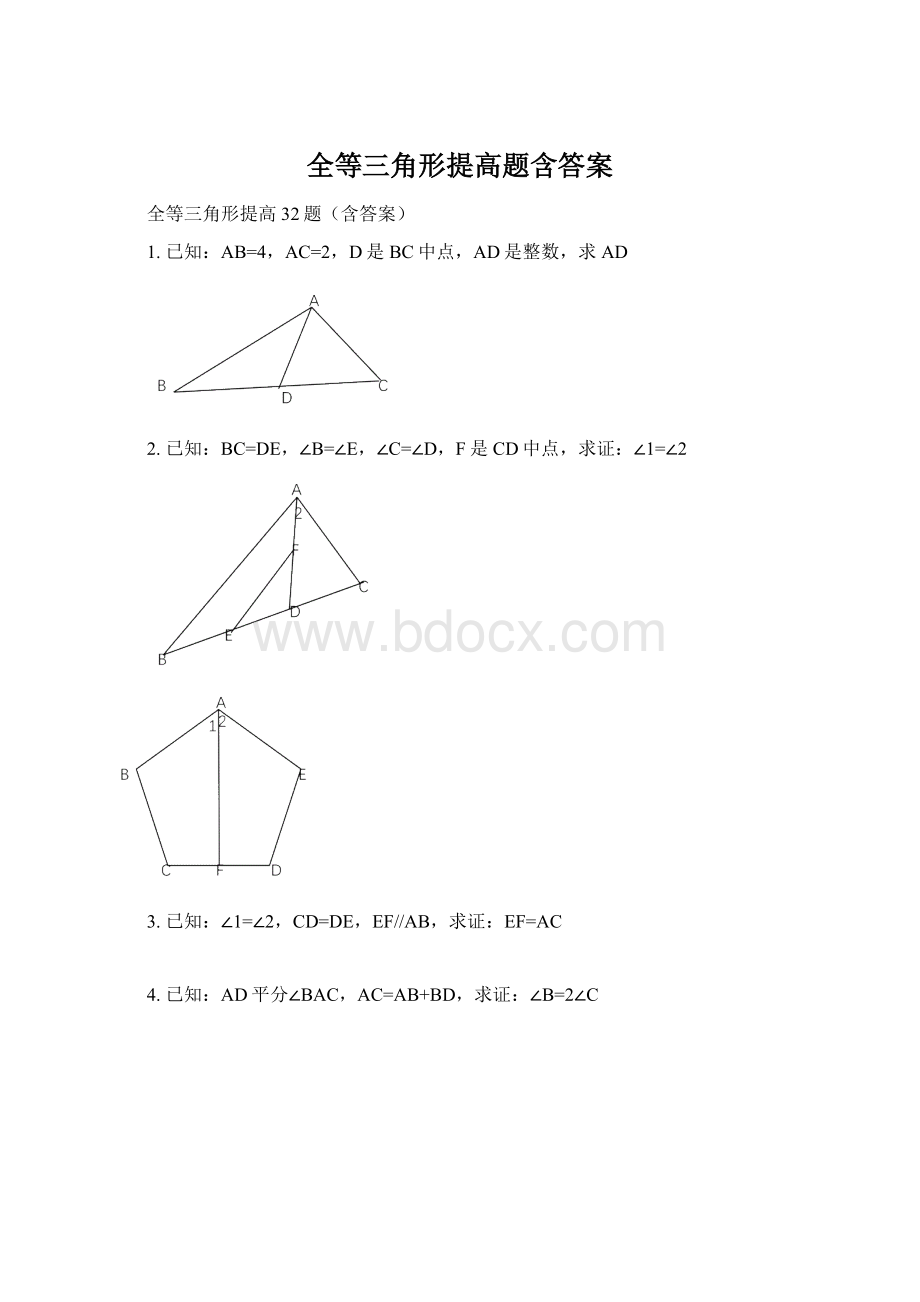
求证：

BC=AB+DC。

7.已知：

AB//ED，∠EAB=∠BDE，AF=CD，EF=BC，求证：

∠F=∠C

8．如图，在△ABC中，BD=DC，∠1=∠2，求证：

AD⊥BC．

9．如图，OM平分∠POQ，MA⊥OP,MB⊥OQ，A、B为垂足，AB交OM于点N．

∠OAB=∠OBA

10．如图，已知AD∥BC，∠PAB的平分线与∠CBA的平分线相交于E，CE的连线交AP于D．求证：

AD+BC=AB．

11．如图，△ABC中，AD是∠CAB的平分线，且AB=AC+CD，求证：

∠C=2∠B

12．如图①，E、F分别为线段AC上的两个动点，且DE⊥AC于E，BF⊥AC于F，若AB=CD，AF=CE，BD交AC于点M．

（1）求证：

MB=MD，ME=MF

（2）当E、F两点移动到如图②的位置时，其余条件不变，上述结论能否成立？

若成立请给予证明；

若不成立请说明理由．

13．已知：

如图，DC∥AB，且DC=AE，E为AB的中点，

△AED≌△EBC．

（2）观看图前，在不添辅助线的情况下，除△EBC外，请再写出两个与△AED的面积相等的三角形．（直接写出结果，不要求证明）：

14．如图，△ABC中，∠BAC=90度，AB=AC，BD是∠ABC的平分线，BD的延长线垂直于过C点的直线于E，直线CE交BA的延长线于F．

BD=2CE．

15、如图：

AE、BC交于点M，F点在AM上，BE∥CF，BE=CF。

AM是△ABC的中线。

16、AB=AC，DB=DC，F是AD的延长线上的一点。

BF=CF

17、如图：

AB=CD，AE=DF，CE=FB。

AF=DE。

18..公园里有一条“Z”字形道路ABCD，如图所示，其中AB∥CD，在AB，CD，BC三段路旁各有一只小石凳E，F，M，且BE＝CF，M在BC的中点，试说明三只石凳E，F，M恰好在一条直线上.

19．已知：

点A、F、E、C在同一条直线上，AF＝CE，BE∥DF，BE＝DF．求证：

△ABE≌△CDF．

20．已知：

如图，AB=AC，BD⊥AC，CE⊥AB，垂足分别为D、E，BD、CE相交于点F，

BE=CD．

21.已知：

如图,ACBC于C,DEAC于E,ADAB于A,BC=AE．若AB=5,

求AD的长？

22．如图：

AB=AC，ME⊥AB，MF⊥AC，垂足分别为E、F，ME=MF。

MB=MC

23．在△ABC中，，，直线经过点，且于，于.

（1）当直线绕点旋转到图1的位置时，求证：

①≌；

②；

（2）当直线绕点旋转到图2的位置时，

（1）中的结论还成立吗？

若成立，请给出证明；

若不成立，说明理由.

24．如图所示，已知AE⊥AB，AF⊥AC，AE=AB，AF=AC。

（1）EC=BF；

（2）EC⊥BF

E

B

M

C

F

25．如图：

BE⊥AC，CF⊥AB，BM=AC，CN=AB。

（1）AM=AN；

（2）AM⊥AN。

26．如图,已知∠A=∠D,AB=DE,AF=CD,BC=EF.求证:

BC∥EF

27．如图,已知AC∥BD，EA、EB分别平分∠CAB和∠DBA，CD过点E，则AB与AC+BD相等吗？

请证明。

28、如图,已知:

AD是BC上的中线,且DF=DE．求证:

BE∥CF．

29、已知：

如图，AB＝CD，DE⊥AC，BF⊥AC，E，F是垂足，．

．

30、如图，已知AC⊥AB，DB⊥AB，AC＝BE，AE＝BD，试猜想线段CE与DE的大小与位置关系，并证明

31、如图，已知AB＝DC，AC＝DB，BE＝CE，求证：

AE＝DE.

32．如图9所示，△ABC是等腰直角三角形，∠ACB＝90°

，AD是BC边上的中线，过C作AD的垂线，交AB于点E，交AD于点F，求证：

∠ADC＝∠BDE．

答案

1.延长AD到E,使DE=AD,则△ADC≌△EBD∴BE=AC=2在△ABE中,AB-BE<

AE<

AB+BE∴10-2<

2AD<

10+24<

AD<

6又AD是整数,则AD=5

2.证明：

连接BF和EF。

∵BC=ED,CF=DF,∠BCF=∠EDF。

∴△BCF≌△EDF（边角边）。

∴BF=EF,∠CBF=∠DEF。

连接BE。

在△BEF中,BF=EF。

∴∠EBF=∠BEF。

又∵∠ABC=∠AED。

∴∠ABE=∠AEB。

∴AB=AE。

在△ABF和△AEF中，

AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF。

∴△ABF≌△AEF

∴∠BAF=∠EAF（∠1=∠2）。

3.证明：

过E点，作EG//AC，交AD延长线于G则∠DEG=∠DCA，∠DGE=∠2

又∵CD=DE∴△ADC≌△GDE（AAS）∴EG=AC∵EF∥AB∴∠DFE=∠1∵∠1=∠2

∴∠DFE=∠DGE∴EF=EG∴EF=AC

4.证明：

在AC上截取AE=AB，连接ED∵AD平分∠BAC∴∠EAD=∠BAD

又∵AE=AB，AD=AD∴⊿AED≌⊿ABD（SAS）∴∠AED=∠B，DE=DB∵AC=AB+BD

AC=AE+CE∴CE=DE∴∠C=∠EDC∵∠AED=∠C+∠EDC=2∠C∴∠B=2∠C

5.证明：

在AE上取F，使EF＝EB，连接CF∵CE⊥AB∴∠CEB＝∠CEF＝90°

∵EB＝EF，CE＝CE，∴△CEB≌△CEF∴∠B＝∠CFE∵∠B＋∠D＝180°

，∠CFE＋∠CFA＝180°

∴∠D＝∠CFA∵AC平分∠BAD∴∠DAC＝∠FAC

又∵AC＝AC∴△ADC≌△AFC（SAS）∴AD＝AF∴AE＝AF＋FE＝AD＋BE

6.证明:

在BC上截取BF=BA,连接EF.

∵∠ABE=∠FBE,BE=BE,∴⊿ABE≌ΔFBE（SAS）,∠EFB=∠A;

AB平行于CD,∴∠A+∠D=180°

;

又∵∠EFB+∠EFC=180°

∴∠EFC=∠D;

又∵∠FCE=∠DCE,CE=CE,∴⊿FCE≌ΔDCE（AAS）,FC=CD.∴BC=BF+FC=AB+CD.

7.∵AB∥ED,AE∥BD∴AE=BD,又∵AF=CD,EF=BC∴△AEF≌△DCB，

∴∠C=∠F

8.延长AD至H交BC于H;

BD=DC;

∴∠DBC=∠DCB;

∠1=∠2;

∠DBC+∠1=∠DCB+∠2;

∠ABC=∠ACB;

∴AB=AC;

△ABD≌△ACD;

∠BAD=∠CAD;

AD是等腰三角形的顶角平分线∴AD⊥BC

9.∵AOM与MOB都为直角三角形、共用OM，且∠MOA=∠MOB∴MA=MB

∴∠MAB=∠MBA∵∠OAM=∠OBM=90度∴∠OAB=90-∠MAB∠OBA=90-∠MBA

∴∠OAB=∠OBA

10.证明：

做BE的延长线，与AP相交于F点，∵PA∥BC

∴∠PAB+∠CBA=180°

，又∵，AE，BE均为∠PAB和∠CBA的角平分线

∴∠EAB+∠EBA=90°

∴∠AEB=90°

，EAB为直角三角形

在△ABF中，AE⊥BF，且AE为∠FAB的角平分线∴△FAB为等腰三角形，AB=AF,BE=EF在△DEF与△BEC中，∠EBC=∠DFE,且BE=EF，∠DEF=∠CEB，

∴△DEF≌△BEC，∴DF=BC∴AB=AF=AD+DF=AD+BC

11.证明：

在AB上找点E，使AE=AC∵AE=AC，∠EAD=∠CAD，AD=AD

∴△ADE≌△ADC。

DE=CD，∠AED=∠C∵AB=AC+CD，∴DE=CD=AB-AC=AB-AE=BE

∠B=∠EDB∠C=∠B+∠EDB=2∠B

12.分析：

通过证明两个直角三角形全等，即Rt△DEC≌Rt△BFA以及垂线的性质得出四边形BEDF是平行四边形．再根据平行四边形的性质得出结论．

解：

（1）连接BE，DF．∵DE⊥AC于E，BF⊥AC于F，，∴∠DEC=∠BFA=90°

，DE∥BF，在Rt△DEC和Rt△BFA中，∵AF=CE，AB=CD，∴Rt△DEC≌Rt△BFA，

∴DE=BF．∴四边形BEDF是平行四边形．∴MB=MD，ME=MF；

（2）连接BE，DF．∵DE⊥AC于E，BF⊥AC于F，，∴∠DEC=∠BFA=90°

∴DE=BF．∴四边形BEDF是平行四边形．∴MB=MD，ME=MF．

13.

（1）∵DC∥AE，且DC=AE，∴四边形AECD是平行四边形。

于是知AD=EC，且∠EAD=∠BEC。

由AE=BE，∴△AED≌△EBC。

（2）△AEC、△ACD、△ECD都面积相等。

14.证明：

延长BA、CE，两线相交于点F∵BE⊥CE∴∠BEF=∠BEC=90°

在△BEF和△BEC中∠FBE=∠CBE,BE=BE,∠BEF=∠BEC∴△BEF≌△BEC（ASA）

∴EF=EC∴CF=2CE∵∠ABD+∠ADB=90°

∠ACF+∠CDE=90°

又∵∠ADB=∠CDE

∴∠ABD=∠ACF在△ABD和△ACF中∠ABD=∠ACF,AB=AC,∠BAD=∠CAF=90°

∴△ABD≌△ACF（ASA）∴BD=CF∴BD=2CE

15.证明：

∵BE∥CF∴∠E=∠CFM，∠EBM=∠FCM∵BE=CF∴△BEM≌△CFM

∴BM=CM∴AM是△ABC的中线.

16.证明：

在△ABD与△ACD中AB=ACBD=DCAD=AD∴△ABD≌△ACD

∴∠ADB=∠ADC∴∠BDF=∠FDC在△BDF与△FDC中BD=DC

∠BDF=∠FDCDF=DF∴△FBD≌△FCD∴BF=FC

17.∵AB=DCAE=DFCE=FBCE+EF=EF+FB∴△ABE≌△CDF

∵∠DCB=∠ABFAB=DCBF=CE∴△ABF≌△CDE∴AF=DE

18.证：

∵AB平行CD（已知）∴∠B=∠C（两直线平行，内错角相等）

∵M在BC的中点（已知）∴EM=FM（中点定义）在△BME和△CMF中

BE=CF（已知）∠B=∠C（已证）EM=FM（已证）△BME全等与△CMF（SAS）

∴∠EMB=∠FMC（全等三角形的对应角相等）∴∠EMF=∠EMB+∠BMF=∠FMC+∠BMF=∠BMC=180°

（等式的性质）∴E，M，F在同一直线上

19.证明：

∵AF=CE∴AF+EF=CE+EF∴AE=CF∵BE//DF∴∠BEA=∠DFC

又∵BE=DF∴△ABE≌△CDF（SAS）

20.证明：

∵AB=AC，∴∠EBC=∠DCB∵BD⊥AC，CE⊥AB∴∠BEC=∠CDBBC=CB（公共边）∴△EBC≌△DCB∴BE＝CD

21.∠C=∠E=90度∠B=∠EAD=90度-∠BACBC=AE△ABC≌△DAEAD=AB=5