扬州市高邮市2016年中考数学三模试卷含答案解析Word文件下载.doc
《扬州市高邮市2016年中考数学三模试卷含答案解析Word文件下载.doc》由会员分享,可在线阅读,更多相关《扬州市高邮市2016年中考数学三模试卷含答案解析Word文件下载.doc(27页珍藏版)》请在冰豆网上搜索。
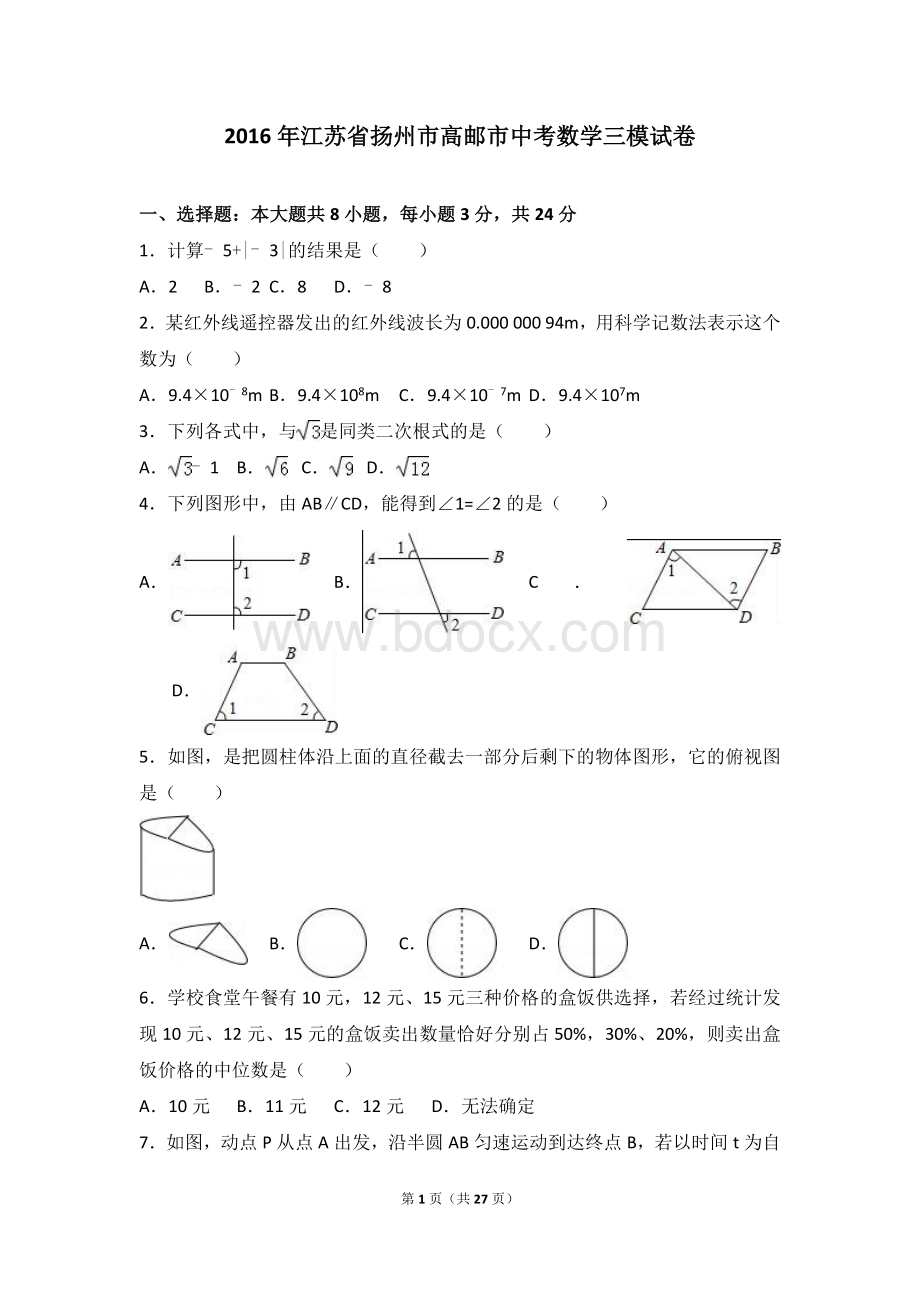
A.5 B.6 C.7 D.8
二、填空题:
本大题共10小题,每小题3分,共30分
9.写出绝对值小于2的一个负数:
.
10.分解因式x2(x﹣2)+4(2﹣x)= .
11.若等腰三角形的一个外角的度数为40°
,则这个等腰三角形顶角的度数是 .
12.在Rt△ABC中,∠C=90°
,点G是Rt△ABC的重心,如果CG=6,那么斜边AB的长等于 .
13.某校射击队从甲、乙、丙、丁四人中选拔一人参加市运会射击比赛.在选拔赛中,每人射击10次,他们10次成绩的平均数及方差如下表所示.
甲
乙
丙
丁
平均数/环
9.7
9.5
方差/环2
5.1
4.7
4.5
请你根据表中数据选一人参加比赛,最合适的人选是 .
14.如图,若用若干个全等的等腰梯形拼成了一个平行四边形,则一个等腰梯形中,最大的内角是 .
15.如图,点C′与半圆上的点C关于直径AB成轴对称.若∠AOC=40°
,则∠CC′B= °
.
16.如图,三个全等的小矩形沿“橫﹣竖﹣橫”排列在一个大矩形中,若这个大矩形的周长为2016cm,则一个小矩形的周长等于 cm.
17.在二次函数y=﹣x2+bx+c中,函数y与自变量x的部分对应值如下表:
x
﹣3
﹣2
﹣1
1
2
3
4
5
6
y
﹣14
﹣7
m
n
﹣23
则m、n的大小关系为m n.(填“<”,“=”或“>”)
18.若函数y=x2﹣3|x﹣1|﹣4x﹣3﹣b(b为常数)的图象与x轴恰好有三个交点,则常数b的值为 .
三、解答题:
本大题共10小题,共96分
19.计算:
﹣32+﹣(cos30°
﹣1)0﹣(﹣)﹣3+82×
0.1252.
20.先化简,再求值:
÷
(m﹣1﹣),其中m=﹣3.
21.为了解高邮市6000名九年级学生英语口语考试成绩的情况,从中随机抽取了部分学生的成绩(满分30分,得分均为整数),制成下表:
分数段(x分)
x≤10
11≤x≤15
16≤x≤20
21≤x≤25
26≤x≤30
人 数
10
15
35
112
128
(1)本次抽样调查共抽取了 名学生;
(2)若用扇形统计图表示统计结果,则分数段为x≤10的人数所对应扇形的圆心角为 °
;
(3)学生英语口语考试成绩的众数 落在11≤x≤15的分数段内;
(填“会”或“不会”)
(4)若将26分以上(含26)定为优秀,请估计该区九年级考生成绩为优秀的人数.
22.学校为参加高邮市“五运会”广播操表演,准备从七、八、九三个年级分别选送到位的一男、一女共6名备选人中,每个年级随机选出1名学生,共3名学生担任领操员
(1)选出3名领操员中,男生的人数可能是 ;
(2)求选出“两男一女”3名领操员的概率.
23.一家文具超市营业员的流水账记录;
五月一日卖出15本笔记本和5只计算器,收入225元,五月二日以同样的价格卖出同样的3本笔记本和6只计算器,收入285元,请你用二元一次方程组的知识进行分析,这个记录是否有错误?
24.如图,在平面直角坐标系中,一次函数y=kx+b的图象与x轴交于点A(﹣1,0),与反比例函数y=在第一象限内的图象交于点B(,n).连接OB,若S△AOB=1.
(1)求反比例函数与一次函数的关系式;
(2)直接写出不等式组的解集.
25.如图,△ABC中,AB=4,AC=2,BC=2,以BC为直径的半圆交AB于点D,以A为圆心,AC为半径的扇形交AB于点E.
(1)以BC为直径的圆与AC所在的直线有何位置关系?
请说明理由;
(2)求图中阴影部分的面积(结果可保留根号和π).
26.如图,已知在△ABC中,AB=AC,tan∠B=2,BC=4,D为BC边的中点,点E在BC边的延长线上,且CE=BC,连接AE,F为线段AE的中点
(1)求线段CF的长;
(2)求∠CAE的正弦值.
27.小颖妈妈的网店加盟了“小神龙”童装销售,有一款童装的进价为60元/件,售价为100元/件,因为刚加盟,为了增加销量,准备对大客户制定如下“促销优惠”方案:
若一次购买数量超过10件,则每增加一件,所有这一款童装的售价降低1元/件,例如一次购买11件时,这11件的售价都为99元/件,但最低售价为80元/件,一次购买这一款童装的售价y元/件与购买量x件之间的函数关系如图.
(1)一次购买20件这款童装的售价为 元/件;
图中n的值为 ;
(2)设小颖妈妈的网店一次销售x件所获利润为w元,求w与x之间的函数关系式;
(3)小颖通过计算发现:
卖25件可以赚625元,而卖30件只赚600元,为了保证销量越大利润就越大,在其他条件不变的情况下,求最低售价应定为多少元/件?
28.如图,已知矩形ABCD中,AB=4cm,BC=6cm,动点P从点C开始,以1cm/s的速度在BC的延长线上向右匀速运动,连接AP交CD边于点E,把射线AP沿直线AD翻折,交CD的延长线于点Q,设点P的运动时间为t.
(1)若DQ=3cm,求t的值;
(2)设DQ=y,求出y与t的函数关系式;
(3)当t为何值时,△CPE与△AEQ的面积相等?
(4)在动点P运动过程中,△APQ的面积是否会发生变化?
若变化,求出△APQ的面积S关于t的函数关系式;
若不变,说明理由,并求出S的定值.
参考答案与试题解析
【考点】有理数的加法;
绝对值.
【分析】根据绝对值的性质,可化简绝对值,根据异号两数相加,取绝对值较大加数的符号,并用较大的绝对值减较小的绝对值,可得答案.
【解答】解:
原式=﹣5+3=﹣(5﹣3)=﹣2,
故选:
B.
【考点】科学记数法—表示较小的数.
【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×
10﹣n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.
0.00000094m=9.4×
10﹣7m,
C.
【考点】同类二次根式.
【分析】先化简二次根式,再判定即可.
A、不是同类二次根式,错误;
B、不是同类二次根式,错误;
C、,不是同类二次根式,错误;
D、是同类二次根式,正确;
故选D
【考点】平行线的判定与性质.
【分析】根据平行线的性质求解即可求得答案,注意掌握排除法在选择题中的应用.
A、∵AB∥CD,
∴∠1+∠2=180°
,
故A错误;
B、∵AB∥CD,
∴∠1=∠3,
∵∠2=∠3,
∴∠1=∠2,
故B正确;
C、∵AB∥CD,
∴∠BAD=∠CDA,
若AC∥BD,可得∠1=∠2;
故C错误;
D、若梯形ABCD是等腰梯形,可得∠1=∠2,
故D错误.
【考点】简单组合体的三视图;
截一个几何体.
【分析】根据俯视图是从上向下看得到的平面图形,切口经过直径也能看到解答.
∵圆柱体沿上面的直径截去一部分,
∴它的俯视图是有直径的圆.
故选D.
【考点】中位数.
【分析】根据中位数的定义先按从小到大的顺序排列起来,再找出最中间两个数的平均数即可得出答案.
∵10元、12元、15元的盒饭卖出数量恰好分别占50%,30%、20%,
∴最中间的两个数是10元、12元,
∴中位数是10和12的平均数,(10+12)÷
2=11(元);
故选B.
【考点】动点问题的函数图象.
【分析】点P在运动过程中,∠AOP的角度随点P的运动而增大,故面积S呈现的是直线上升趋势,从而可以得出解答.
点P与点A重合时,扇形OAP的面积为O,故可知B错误;
设∠AOP的角度为n,当点P沿半圆AB匀速运动过程中,n随着t的增大而增大,而圆的半径不变,则可知扇形面积OAP是在逐步增大的.
即S=(0≤n≤180°
)
当点P到达终点B点时,∠AOB=180°
,此时扇形面积最大.故可知A、D错误.
【考点】正多边形和圆.
【分析】首先求得正五边形的每一个内角的度数,即可求得其对的圆心角度数,继而求得答案.
如图,圆心角为∠1,
∵∵五边形的内角和为:
(5﹣2)×
180°
=3×
=540°
∴五边形的每一个内角为:
540°
5=108°
∴∠1=108°
×
2﹣180°
=216°
﹣180°
=36°
∵360°
36°
=10,
∴他要完成这一圆环共需10个全等的五边形.
∴要完全拼成一个圆环还需要的正五边形个数是:
10﹣3=7.
故选C.
﹣1(答案不唯一) .
【考点】绝对值;
正数和负