李正元高等数学强化讲义Word格式文档下载.doc

李正元高等数学强化讲义Word格式文档下载.doc

《李正元高等数学强化讲义Word格式文档下载.doc》由会员分享，可在线阅读，更多相关《李正元高等数学强化讲义Word格式文档下载.doc（118页珍藏版）》请在冰豆网上搜索。

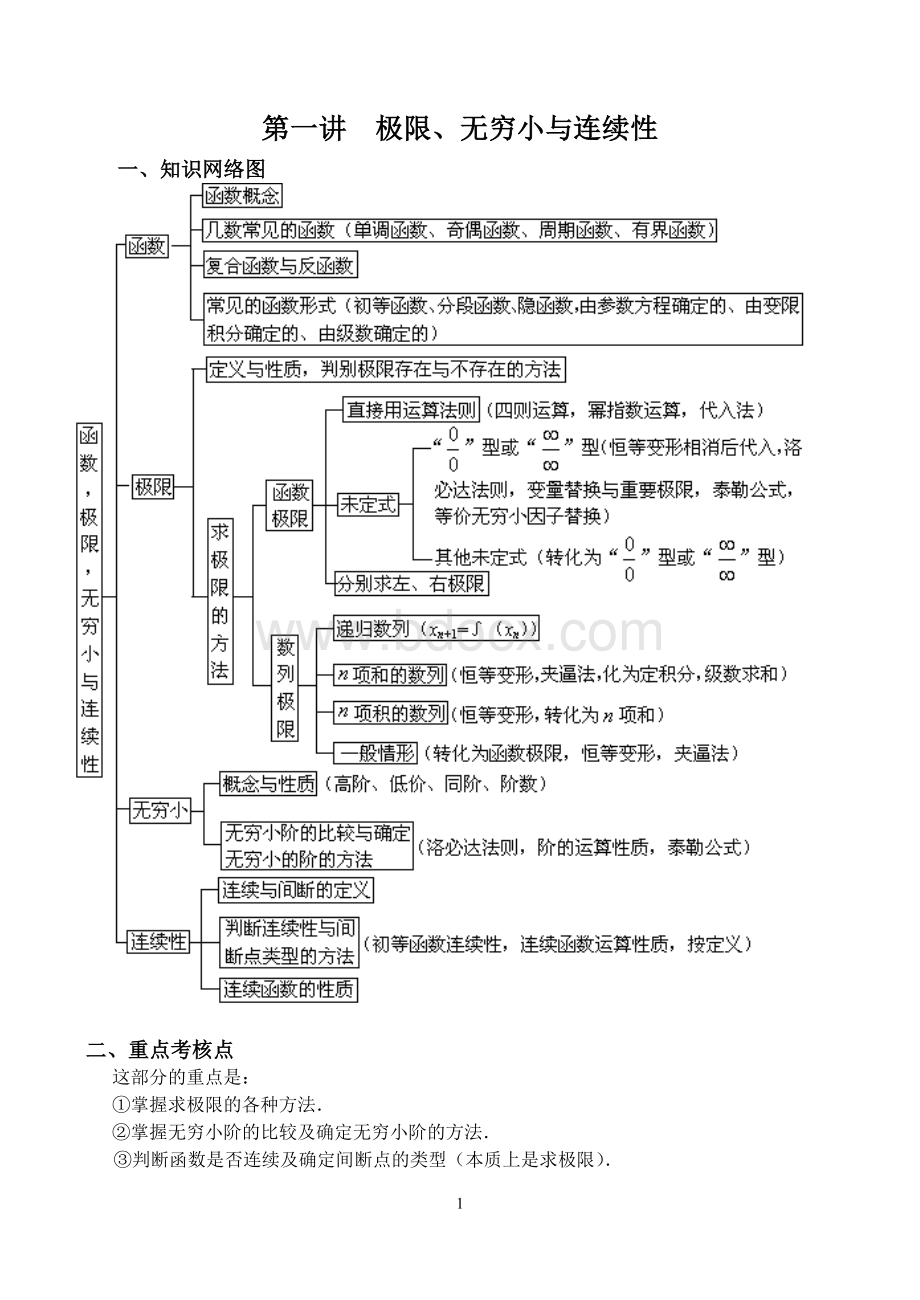
设，则数列｛xn｝有界，即存在M＞0，使得｜xn｜≤M（n=1，2，3，…）．

设则函数f（x）在x=x0的某空心邻域中有界，即存在δ＞0和M＞0，使得当0＜｜x－x0｜＜δ时有｜f（x）｜≤M．对其他类型的函数极限也有类似的结论．

2求极限的方法

1．极限的四则运算法则及其推广设，则

只要设存在或是无穷大量，上面的四则运算法则可以推广到除“”，“”，“0·

∞”，“∞－∞”四种未定式以外的各种情形．即：

1°

设，则.（）又B≠0，则．2°

设，当x→x0时局部有界，（即，使得时），则．

设，当x→x0时｜g（x）｜局部有正下界，（即$δ＞0，b＞0使得0＜｜x－x0｜＜δ时｜g（x）｜≥b＞0），则．

3°

设，，则，又$δ＞0使得0＜｜x－x0｜＜δ时f（x）g（x）＞0，则．

4°

设，x→x0时g（x）局部有界，则（无穷小量与有界变量之积为无穷小．）

2．幂指函数的极限及其推广

设

只要设存在或是无穷大量,上面的结果可以推广到除“1∞”，“00”及“∞0”三种未定式以外的各种情形．这是因为仅在这三个情况下是“0·

∞”型未定式．

1°

设=0（0＜｜x－｜＜δ时f（x）＞0），，则

2°

设=A＞0，A≠1，=+∞，则

设=+∞，，则

【例1】设

【分析】

【例2】设｛an｝，｛bn｝，｛cn｝均为非负数列，且则必有

（A）an＜bn对任意n成立．（B）bn＜cn对任意n成立．

（C）极限不存在．（D）不存在．

用相消法求或型极限

【例1】求

【解】作恒等变形，分子、分母同乘

．

【例2】求

【解】作恒等变形，分子、分母同除得

利用洛必达法则求极限

【例1】设f（x）在x=0有连续导数，又

求．

【例2】求．

【例3】求．

【例4】求．

【例5】若，则．

【例6】求．

【例7】设a＞0，b≠0为常数且，则（a，b）=__________．

【分析】∞－∞型极限．

因此（a，b）=．

分别求左、右极限的情形，分别求的情形

【例1】设，求．【例2】求

利用函数极限求数列极限

【例1】求．【例2】求．

【解1】

转化为求

【解2】用求指数型极限的一般方法．

转化为求

（等价无穷小因子替换），余下同前．

3无穷小和它的阶

1．无穷小、极限、无穷大及其联系

（1）无穷小与无穷大的定义

（2）极限与无穷小，无穷小与无穷大的关系

其中

o

（1）表示无穷小量．

在同一个极限过程中，u是无穷小量（u≠0）Þ

是无穷大量．反之若u是无穷大量，则是无穷小量．

2．无穷小阶的概念

（1）定义同一极限过程中，a（x），b（x）为无穷小，

设

定义设在同一极限过程中a（x），b（x）均为无穷小，a（x）为基本无穷小，若存在正数k与常数使得称b（x）是a（x）的k阶无穷小，特别有，称x→x0时b（x）是（x－x0）的k阶无穷小．

（2）重要的等价无穷小

x→0时sinx~x，tanx~x，㏑（1+x）~x，ex－1~x；

ax－1~xlna，arcsinx~x，

arctanx~x；

（1+x）a―1~ax，1―cosx~．

（3）等价无穷小的重要性质

在同一个极限过程中

若a~b，b~gÞ

a~g．

a~bÛ

a=b+o（b）

在求“”型与“0·

∞”型极限过程中等价无穷小因子可以替换

【例1】求．

【例2】设．

【分析】由已知条件及

．又在x=0某空心邻域f（x）≠0Þ

，又3x－1~xln3．于是

．

【例3】设x→a时a（x），b（x）分别是x－a的n阶与m阶无穷小，又，则x→a时

（1）a（x）h（x）是x－a的__________阶无穷小．

（2）a（x）b（x）是x－a的__________阶无穷小．

（3）n＜m时，a（x）±

b（x）是x－a的__________阶无穷小．

（4）n＞m时是x－a的__________阶无穷小．

（5）k是正整数时，ak是x－a的__________阶无穷小．

以上结论容易按定义证明。

例如，已知，Þ

f（x）g（x）是x－a的n+m阶无穷小．

【例4】设f（x）连续，x→a时f（x）是x－a的n阶无穷小，求证：

是x－a的n+1阶无穷小．

【例5】x→0时，是x的________阶无穷小；

是x的_________阶无穷小；

是x的_________阶无穷小，是x的_________阶无穷小．

【例6】x→0时，下列无穷小中（）比其他三个的阶高，

（A）x2（B）1－cosx（C）（D）x－tanx

【例7】当x→0时，与比较是（）的无穷小．

（A）等价（B）同阶非等价

（C）高阶（D）低阶

4连续性及其判断

1．连续性概念

（1）连续的定义：

函数f（x）满足，则称f（x）在点x=x0处连续；

f（x）满足（或，则称f（x）在x=x0处右（或左）连续．

若f（x）在（a，b）内每一点连续，则称f（x）在（a，b）内连续；

若f（x）在（a，b）内连续，且在x=a处右连续，在点x=b处左连续，则称f（x）在[a，b]上连续．

（2）单双侧连续性

f（x）在x=x0处连续Û

f（x）在x=x0处既左连续，又右连续．

（3）间断点的分类：

设f（x）在点x=x0的某一空心邻域内有定义，且x0是f（x）的间断点．

若f（x）在点x=x0处的左、右极限f（x0－0）与f（x0+0）存在并相等，但不等于函数值f（x0）或f（x）在x0无定义，则称点x0是可去间断点；

若f（x）在点x=x0处的左、右极限f（x0－0）与f（x0+0）存在但不等，则称点x0是跳跃间断点：

它们统称为第一类间断点．

若f（x）在点x=x0处的左、右极限f（x0－0）与f（x0+0）至少有一个不存在，则称点x0为第二类间断点．

2．函数连续性与间断点类型的判断：

若f（x）为初等函数，则f（x）在其定义域区间D上连续，即当开区间（a，b）Ì

D，则f（x）在（a，b）内连续；

当闭区间[c，d]Ì

D，则f（x）在[c，d]上连续．若f（x）是非初等函数或不清楚它是否为初等函数，则用连续的定义和连续性运算法则（四则运算，反函数运算与复合运算）来判断．当f（x）为分段函数时，在其分界点处则需按定义或分别判断左、右连续性．

判断f（x）的间断点的类型，就是求极限．

3．有界闭区间[a，b]上连续函数的性质：

最大值和最小值定理：

设f（x）在闭区间[a，b]上连续，则存在ξ和ηÎ

[a，b]，使得

f（ξ）≤f（x）≤f（η），（a≤x≤b）

有界性定理：

设f（x）在闭区间[a，b]上连续，则存在M＞0，使得

｜f（x）｜≤M，（a≤x≤b）

介值定理：

设函数f（x）在闭区间[a，b]上连续，且f（a）≠f（b），则对f（a）与f（b）之间的任意一个数c，在（a，b）内至少存在一点ξ，使得f（ξ）=c

推论1（零值定理）：

设f（x）在闭区间[a，b]上连续，且f（a）f（b）＜0，则在（a，b）内至少存在一点ξ，使得f（ξ）=0

推论2：

设f（x）在闭区间[a，b]上连续，且m和M分别是f（x）在[a，b]上最小值和最大值，若m＜M，则f（x）在[a，b]上的值域为[m，M]．

【例1】函数在下列哪个区间内有界．

（A）（－1，0）．（B）（0，1）．（C）（1，2）．（D）（2，3）．

【分析一】这里有界．只须考察，g（x）是初等函数，它在定义域（x≠1，x≠2）上连续，有界闭区间上连续函数有界，[－1，0]Ì

定义域，g（x）在[－1，0]有界，选（A）．

【分析二】设h（x）定义在（a，b）上，若或，则h（x）在（a，b）无界．因，Þ

在（0，1），（1，2），（2，3）均无界．选（A）．

【例2】设，

讨论y=f（g（x））的连续性，若有间断点并指出类型．

【分析与解法1】先求f（g（x））的表达式．

Þ

在（－∞，1），（1，2），（2，5），（5，+∞），f（g（x））分别与初等函数相同，故连续．x=2或5时可添加等号，左、右连接起来，即左连续又右连续Þ

f（g（x））在x=2或5连续．x=1时

Þ

x=1是f（g（x））的第一类间断点（跳跃间断点）．

【分析与解法2】不必求出f（g（x））的表达式．

g（x）的表达式中，x=2或5处可添加等号，左、右连接起来Þ

g（x）在（－∞，+∞）处处连续．

，u≠1时连续．

u=g（x）=1Û

x=1

因此，x≠1时由连续函数的复合函数是连续的Þ

f（g（x））连续.x=1时

x=1是f（g（x））的第一类间断点．

第二讲一元函数微分学的概念、计算及简单应用

二、重点考核点

这部分的重点是

①导数与微分的定义、几何意义，讨论函数的可导性及导函数的连续性，特别是分段函数，可导与连续的关系．

②按定义或微分法则求各种类型函数的一、