二模试题分实验操作题学生版Word文档格式.doc
《二模试题分实验操作题学生版Word文档格式.doc》由会员分享,可在线阅读,更多相关《二模试题分实验操作题学生版Word文档格式.doc(9页珍藏版)》请在冰豆网上搜索。
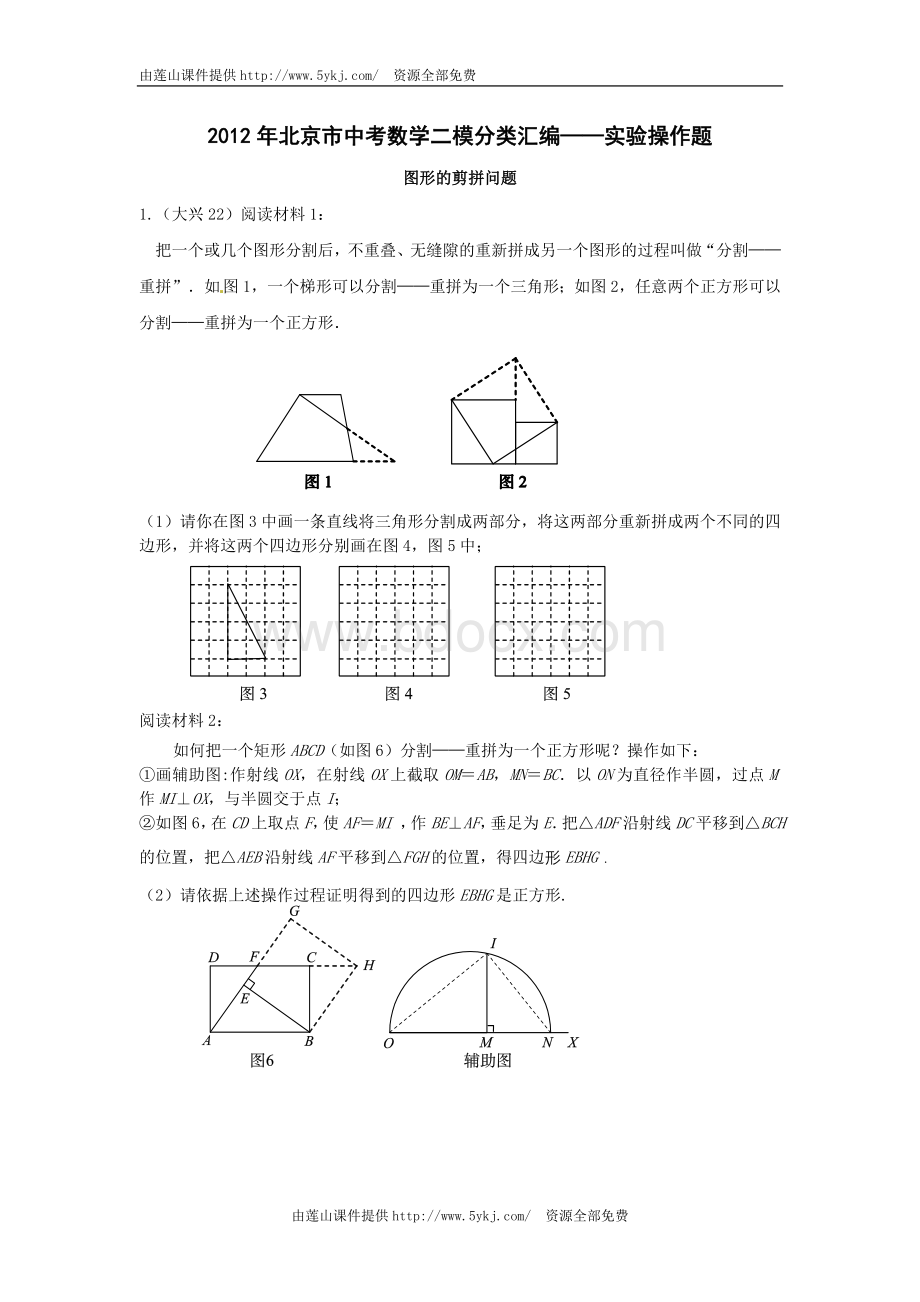
②“谁能将下面的任意四边形分割后,再拼成一个平行四边形”.
.经过小组同学动手合作,第3组的小亮同学向大家展示了他们组的分割方法与拼接方案,如图1和图2所示;
请你参考小亮同学的做法,解决下列问题:
(1)“请你将图3再设计一种分割方法,沿分割线剪开后所得的几块图形恰好也能拼成一个矩形”;
(2)“请你设计一种方法,将图4分割后,再拼成一个矩形”.
3.(房山22)⑴阅读下面材料并完成问题:
已知:
直线AD与△ABC的边BC交于点D,
①如图1,当BD=DC时,则S△ABD________S△ADC.(填“=”或“<”或“>”)
图1图2图3
②如图2,当BD=DC时,则.
③如图3,若AD∥BC,则有.(填“=”或“<”或“>”)
⑵请你根据上述材料提供的信息,解决下列问题:
过四边形ABCD的一个顶点画一条直线,把四边形ABCD的面积分成1︰2的两部分.(保留画图痕迹)
4.(西城区22)阅读下列材料
小华在学习中发现如下结论:
图1
如图1,点A,A1,A2在直线l上,当直线l∥BC时,
.
请你参考小华的学习经验画图(保留画图痕迹):
(1)如图2,已知△ABC,画出一个等腰△DBC,使其面积与△ABC面积相等;
(2)如图3,已知△ABC,画出两个Rt△DBC,使其面积与△ABC面积相等(要求:
所画的两个三角形不全等);
(3)如图4,已知等腰△ABC中,AB=AC,画出一个四边形ABDE,使其面积与△ABC面积相等,且一组对边DE=AB,另一组对边BD≠AE,对角∠E=∠B.
图2图3图4
5.(平谷22)在数学活动课上,老师请同学们在一张长为18cm,宽为14cm的长方形纸上剪下一个腰为12cm的等腰三角形(要求等腰三角形的一个顶点与长方形的一个顶点重合,其余两个顶点在长方形的边上).小明同学按老师要求画出了如图
(1)的设计方案示意图,请你画出与小明的设计方案不同的所有满足老师要求的示意图,并通过计算说明哪种情况下剪下的等腰三角形的面积最小(含小明的设计方案示意图).
图形变换操作题
6.(延庆22)阅读下面材料:
阅读下面材料:
小伟遇到这样一个问题:
如图1,在△ABC(其中∠BAC是一个可以变化的角)中,AB=2,AC=4,以BC为边在BC的下方作等边△PBC,求AP的最大值。
小伟是这样思考的:
利用变换和等边三角形将边的位置重新组合.他的方法是以点B为旋转中心将△ABP逆时针旋转60°
得到△A’BC,连接,当点A落在上时,此题可解(如图2).
请你回答:
AP的最大值是.
参考小伟同学思考问题的方法,解决下列问题:
如图3,等腰Rt△ABC.边AB=4,P为△ABC内部一点,
则AP+BP+CP的最小值是.(结果可以不化简)
7.(石景山22)阅读下面材料:
小阳遇到这样一个问题:
如图
(1),O为等边△内部一点,且,求的度数.
图⑴图⑵图⑶
小阳是这样思考的:
图
(1)中有一个等边三角形,若将图形中一部分绕着等边三角形的某个顶点旋转60°
,会得到新的等边三角形,且能达到转移线段的目的.他的作法是:
如图
(2),把△绕点A逆时针旋转60°
,使点C与点B重合,得到△,连结.则△是等边三角形,故,至此,通过旋转将线段OA、OB、OC转移到同一个三角形中.
(1)请你回答:
(2)参考小阳思考问题的方法,解决下列问题:
如图(3),四边形ABCD中,AB=AD,∠DAB=60°
,∠DCB=30°
,AC=5,CD=4.求四边形ABCD的面积.
解:
8.(顺义22)阅读下列材料:
问题:
如图1,P为正方形ABCD内一点,且PA∶PB∶PC=1∶2∶3,求∠APB的度数.
小娜同学的想法是:
不妨设PA=1,PB=2,PC=3,设法把PA、PB、PC相对集中,于是他将△BCP绕点B顺时针旋转90°
得到△BAE(如图2),然后连结PE,问题得以解决.
图2中∠APB的度数为.
请你参考小娜同学的思路,解决下列问题:
如图3,P是等边三角形ABC内一点,已知∠APB=115°
,∠BPC=125°
.
(1)在图3中画出并指明以PA、PB、PC的长度为三边长的一个三角形(保留画图痕迹);
(2)求出以PA、PB、PC的长度为三边长的三角形的各内角的度数分别等于.
图1图2图3
9.(丰台22)小杰遇到这样一个问题:
如图1,在□ABCD中,AE⊥BC于点E,AF⊥CD于点F,连结EF,△AEF的三条高线交于点H,如果AC=4,EF=3,求AH的长.
小杰是这样思考的:
要想解决这个问题,应想办法将题目中的已知线段与所求线段尽可能集中到同一个三角形中.他先后尝试了翻折、旋转、平移的方法,发现可以通过将△AEH平移至△GCF的位置(如图2),可以解决这个问题.
请你参考小杰同学的思路回答:
(1)图2中AH的长等于.
(2)如果AC=a,EF=b,那么AH的长等于.
图1图2
特殊三角形
10.(门头沟22)数学课上,同学们探究发现:
如图1,顶角为36°
的等腰三角形具有一种特性,即经过它某一顶点的一条直线可把它分成两个小等腰三角形.并且对其进行了证明.
(1)证明后,小乔又发现:
下面两个等腰三角形如图2、图3也具有这种特性.请你在
图2、图3中分别画出一条直线,把它们分成两个小等腰三角形,并在图中标出所画等腰三角形两个底角的度数;
(2)接着,小乔又发现:
直角三角形和一些非等腰三角形也具有这样的特性,如:
直角三角形斜边上的中线可以把它分成两个小等腰三角形.请你画出一个具有这种特性的三角形的示意图,并在图中标出此三角形的各内角的度数.(说明:
要求画出的既不是等腰三角形,也不是直角三角形.)
类比学习
11.(昌平22)类比学习:
有这样一个命题:
设x、y、z都是小于1的正数,求证:
x(1-y)+y(1-z)+z(1-x)<1.
小明同学是这样证明的:
如图,作边长为1的正三角形ABC,并分别在其边上截取AD=x,BE=z,CF=y,设△ADF、△CEF和△BDE的面积分别为、、,
则,
,
由++<,
得++<.
所以x(1-y)+y(1-z)+z(1-x)<1.
类比实践:
已知正数、、、,、、、满足====.
求证:
+++<.
12.(海淀22)阅读下面材料:
小明遇到这样一个问题:
我们定义:
如果一个图形绕着某定点旋转一定的角度a(0°
<
a<
360°
)后所得的图形与原图形重合,则称此图形是旋转对称图形.如等边三角形就是一个旋转角为120°
的旋转对称图形.如图1,点O是等边三角形△ABC的中心,D、E、F分别为AB、BC、CA的中点,请你将△ABC分割并拼补成一个与△ABC面积相等的新的旋转对称图形.
图1图2
E3
心形于绕着一定������������������������������������������������������������������������������������������������������������������������
E1
E2
P1
P2
N1
N2
M2
M1
C
B
A
图3
G
F
H
小明利用旋转解决了这个问题,图2中阴影部分所示的图形即是与△ABC面积相等的新的旋转对称图形.
请你参考小明同学解决问题的方法,利用图形变换解决下列问题:
如图3,在等边△ABC中,E1、E2、E3分别为AB、
BC、CA的中点,P1、P2,M1、M2,N1、N2分别为
AB、BC、CA的三等分点.
(1)在图3中画出一个和△ABC面积相等的新的旋转
对称图形,并用阴影表示(保留画图痕迹);
(2)若△ABC的面积为a,则图3中△FGH的面积为.
13.(密云22)定义:
到凸四边形一组对边距离相等,到另一组对边距离也相等的点叫凸四边形的准内点.如图1,,,则点就是四边形的准内点.
(1)如图2,与的角平分线相交于点.
点是四边形的准内点.
(2)分别画出图3平行四边形和图4梯形的准内点(作图工具不限,不写作法,但要有必要的说明).
14.(东城区22)阅读并回答问题:
小亮是一位刻苦学习、勤于思考、勇于创新的同学.一天他在解方程时,突发奇想:
在实数范围内无解,如果存在一个数i,使,那么当时,有i,从而i是方程的两个根.
据此可知:
(1)i可以运算,例如:
i3=i2·
i=-1×
i=-i,则i4=,
i2011=_____________