分支限界法实验单源最短路径Word格式文档下载.docx
《分支限界法实验单源最短路径Word格式文档下载.docx》由会员分享,可在线阅读,更多相关《分支限界法实验单源最短路径Word格式文档下载.docx(12页珍藏版)》请在冰豆网上搜索。
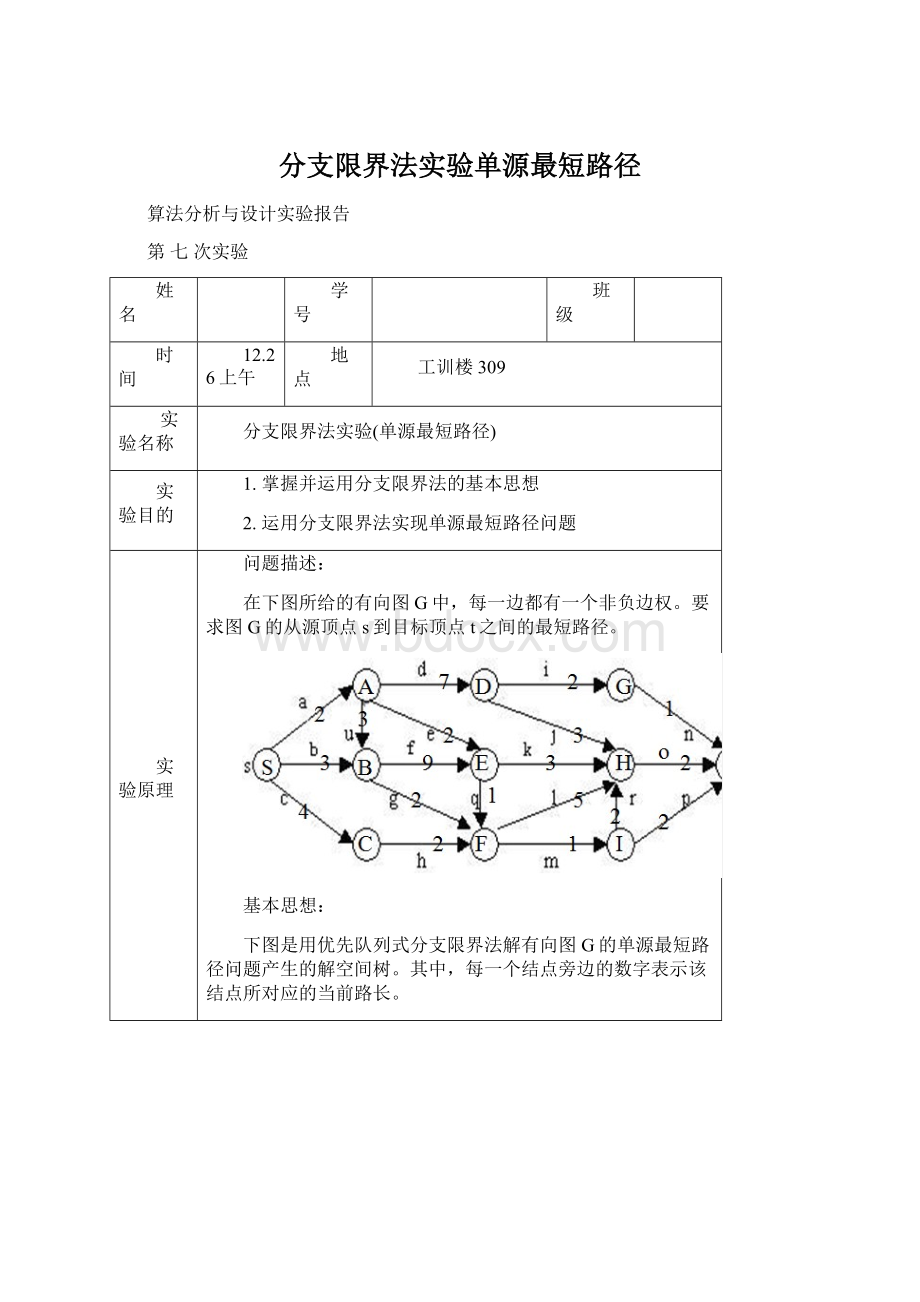
按照优先队列中规定的优先级选取优先级最高的结点成为当前扩展结点。
实验步骤
(1)算法从图G的源顶点s和空优先队列开始。
结点s被扩展后,它的儿子结点被依次插入堆中;
(2)算法每次从堆中取出具有最小当前路长的结点作为当前扩展结点,并依次检查与当前扩展结点相邻的所有顶点;
(3)如果从当前扩展结点i到j有边可达,且从源出发,途经i再到j的所相应路径长度,小于当前最优路径长度,则将该顶点作为活结点插入到活结点优先队列中;
(4)结点扩展过程一直继续到活结点优先队列为空时为止。
关键代码
//单源最短路径问题的优先队列式分支限界法
template<
classType>
voidGraph<
Type>
:
shortest_path(intv)
{
//定义最小堆的容量为1000
MinHeap<
MinHeapNode<
>
H(1000);
//定义源为初始扩展结点
MinHeapNode<
E;
//初始化源结点
E.i=v;
E.length=0;
dist[v]=0;
while(true)//搜索问题的解空间
{
for(intj=1;
j<
=n;
j++)
if((c[E.i][j]!
=0)&
&
(E.length+c[E.i][j]<
dist[j]))
{
//顶点i到顶点j可达,且满足控制约束
//顶点i和j之间有边,且此路径小于原先从源点到j的路径长度
dist[j]=E.length+c[E.i][j];
//更新dist数组
prev[j]=E.i;
//加入活结点优先队列
MinHeapNode<
N;
N.i=j;
N.length=dist[j];
H.Insert(N);
//插入到最小堆中
}
try
H.DeleteMin(E);
//取下一扩展结点
catch(int)
break;
if(H.currentsize==0)//优先队列空
}
}
测试结果
上述有向图的结果:
实验分析
在实验中并没有生成多组数据,进行比较,也没有利用随机生成函数,因为在这种有实际有关联的问题中,利用随机生成函数生成的数据是十分的不合适的,在此我们只需要验证该程序是否正确即可。
分支限界法求单源最短路径问题与回溯法求单源最短路径问题其大致思想是一致的,都是利用解空间树,搜索子集树,回溯法是利用深度优先搜索子集树,而分支限界法是利用广度优先搜索子集树,然后利用队列或优先队列,最小堆存放可扩展的结点,然后将活结点出堆,从而直到堆空为止,找到最优解。
实验心得
在这一章的分支限界法中,与上一章的回溯法很相似,都是利用解空间树进行搜索,从而找到最优解。
不同的是回溯法利用的是深度优先回溯寻找,能够找到所有的最优解;
而分支限界法则是利用广度优先搜索子集树或者排序树,利用队列或者优先级队列的数据结构组织所有满足的结点,这样只要找到一种最优解就可以了,想对于回溯法来说时间上相对利用的没有那么多。
在这一章的学习上,由于会利用最小堆/最大堆,所以代码看起来比较复杂,堆的实现也比较复杂,这是这一章我学习的一个难点,不过正在渐渐攻克。
实验得分
助教签名
附录:
完整代码(分支限界法)
Shorest_path.cpp
//单源最短路径问题分支限界法求解
#include<
iostream>
time.h>
iomanip>
#include"
MinHeap2.h"
usingnamespacestd;
classGraph//定义图类
friendintmain();
public:
voidshortest_path(int);
private:
intn,//图的顶点数
*prev;
//前驱顶点数组
Type**c,//图的邻接矩阵
*dist;
//最短距离数组
};
classMinHeapNode//最小堆中的元素类型为MinHeapNode
friendGraph<
;
operatorint()const{returnlength;
inti;
//顶点编号
Typelength;
//当前路长
//单源最短路径问题的优先队列式分支限界法
while(true)//搜索问题的解空间
//顶点i和j之间有边,且此路径小于原先从源点i到j的路径长度
//更新dist数组
//插入到最小堆中
if(H.currentsize==0)//优先队列空
intmain()
intn=11;
intprev[12]={0,0,0,0,0,0,0,0,0,0,0,0};
//初始化前驱顶点数组
intdist[12]={1000,1000,1000,1000,1000,1000,1000,1000,1000,1000,1000,1000};
//初始化最短距离数组
cout<
<
"
单源图的邻接矩阵如下:
endl;
int**c=newint*[n+1];
for(inti=1;
i<
i++)//输入图的邻接矩阵
c[i]=newint[n+1];
{
cin>
c[i][j];
}
intv=1;
//源结点为1
Graph<
int>
G;
G.n=n;
G.c=c;
G.dist=dist;
G.prev=prev;
clock_tstart,end,over;
//计算程序运行时间的算法
start=clock();
end=clock();
over=end-start;
G.shortest_path(v);
//调用图的最短路径查找算法
//输出从源结点到目的结点的最短路径
从S到T的最短路长是:
dist[11]<
for(inti=2;
i++)//输出每个结点的前驱结点
cout<
prev("
)="
prev[i]<
"
i++)//输出从源结点到其他结点的最短路径长度
从1到"
的最短路长是:
dist[i]<
i++)//删除动态分配时的内存
delete[]c[i];
delete[]c;
c=0;
printf("
Thetimeis%6.3f"
(double)(end-start-over)/CLK_TCK);
//显示运行时间
system("
pause"
);
return0;
MinHeap.h
classGraph;
classT>
classMinHeap//最小堆类
template<
friendclassGraph;
MinHeap(intmaxheapsize=10);
//构造函数,堆的大小是10
~MinHeap(){delete[]heap;
}//最小堆的析构函数
intSize()const{returncurrentsize;
}//Size()返回最小堆的个数
TMax(){if(currentsize)returnheap[1];
}//第一个元素出堆
T>
Insert(constT&
x);
//最小堆的插入函数
DeleteMin(T&
//最小堆的删除函数
voidInitialize(Tx[],intsize,intArraySize);
//堆的初始化
voidDeactivate();
voidoutput(Ta[],intn);
intcurrentsize,maxsize;
T*heap;
voidMinHeap<
output(Ta[],intn)//输出函数,输出a[]数组的元素
i++)
a[i]<
MinHeap<
MinHeap(intmaxheapsize)
maxsize=maxheapsize;
heap=newT[max