八年级数学上第一章勾股定理综合难题1Word格式文档下载.docx

八年级数学上第一章勾股定理综合难题1Word格式文档下载.docx

《八年级数学上第一章勾股定理综合难题1Word格式文档下载.docx》由会员分享，可在线阅读，更多相关《八年级数学上第一章勾股定理综合难题1Word格式文档下载.docx（10页珍藏版）》请在冰豆网上搜索。

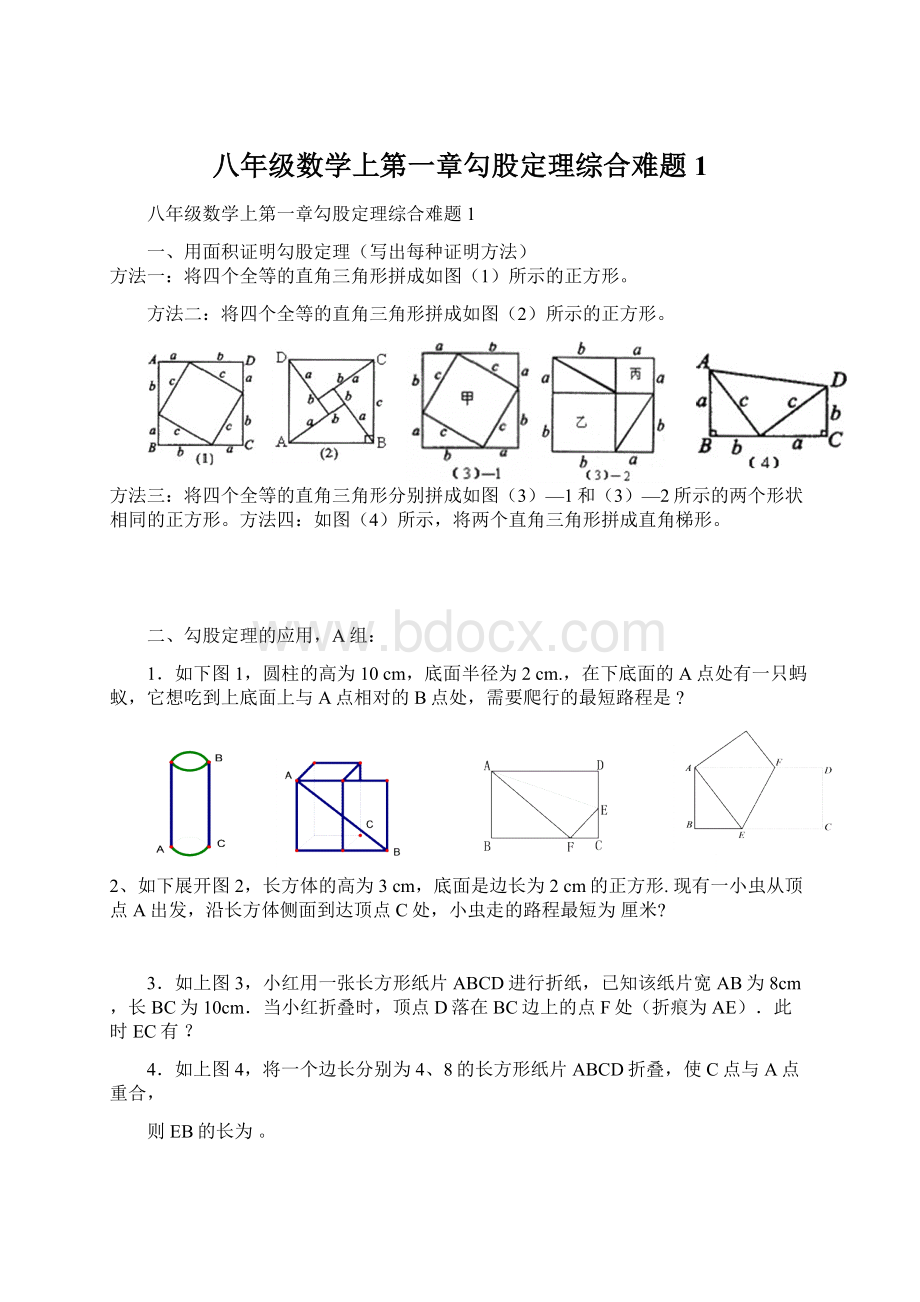
3．如上图3，小红用一张长方形纸片ABCD进行折纸，已知该纸片宽AB为8cm，长BC为10cm．当小红折叠时，顶点D落在BC边上的点F处（折痕为AE）．此时EC有？

4．如上图4，将一个边长分别为4、8的长方形纸片ABCD折叠，使C点与A点重合，

则EB的长为。

5．已知：

如下图1，在△ABC中，∠C=90°

，∠B=30°

，AB的垂直平分线交BC于D，垂足为E，BD=4cm．

则AC的长为．

6、如下图2，有一个直角三角形纸片，两直角边AC=6，BC=8，现将直角边AC沿直线AD折叠，使其落在斜边AB上，且与AE重合，则CD的长为。

7、如上图3，在矩形中，将矩形折叠，使点B与点D重合，落在处，若，则折痕的长为。

8．如下图1，已知：

点E是正方形ABCD的BC边上的点，现将△DCE沿折痕DE向上翻折，使DC落在对角线DB上，则EB∶CE＝_________．

9、如下图2，AD是△ABC的中线，∠ADC＝45o，把△ADC沿AD对折，点C落在C´

的位置，若BC＝2，则BC´

＝_________．

10．如上图3，有一块塑料矩形模板ABCD，长为10cm，宽为4cm，将你手中足够大的直角三角板PHF的直角顶点P落在AD边上（不与A、D重合），在AD上适当移动三角板顶点P：

①能否使你的三角板两直角边分别通过点B与点C？

若能，请你求出这时AP的长；

若不能，请说明理由．②再次移动三角板位置，使三角板顶点P在AD上移动，直角边PH始终通过点B，另一直角边PF与DC的延长线交于点Q，与BC交于点E，自己做出图形，能否使CE＝2cm？

若能，请你求出这时AP的长；

若不能，请你说明理由．

11、如图所示，在中,,且,,求的长.

12、如图，在△ABC中，AB=AC=6，P为BC上任意一点，请用学过的知识试求PC·

PB+PA2的值。

13、如图在Rt△ABC中,，在Rt△ABC的外部拼接一个合适的直角三角形，使得拼成的图形是一个等腰三角形。

如图所示：

要求：

在两个备用图中分别画出两种与示例图不同的拼接方法，在图中标明拼接的直角三角形的三边长（请同学们先用铅笔画出草图，确定后再用0.5mn的黑色签字笔画出正确的图形）

14．如图，A、B两个村子在河CD的同侧，A、B两村到河的距离分别为AC=1km，BD=3km，CD=3km，现在河边CD上建一水厂向A、B两村输送自来水，铺设水管的费用为20000元/千米，请你在CD选择水厂位置O，使铺设水管的费用最省，并求出铺设水管的总费用F。

15．已知：

如下图，△ABC中，∠C=90°

，点O为△ABC的三条角平分线的交点，OD⊥BC，

OE⊥AC，OF⊥AB，点D、E、F分别是垂足，且BC=8cm，CA=6cm，则点O到三边AB，

AC和BC的距离，等于 

cm。

16、如上图2，一个牧童在小河的南4km的A处牧马，而他正位于他的小屋B的西8km北7km处，他想把他的马牵到小河边去饮水，然后回家，他要完成这件事情所走的最短路程是？

17、如图，已知：

，，于P．求证：

．

18、如图所示，某住宅社区在相邻两楼之间修建一个上方是一个半圆，下方是长方形的仿古通道，现有一辆卡车装满家具后，高4米，宽2.8米，请问这辆送家具的卡车能否通过这个通道.

19、a、b为任意正数，且a>

b，求证：

边长为2ab、a2－b2、a2+b2的三角形是直角三角形。

B组;

1．在一棵树的10米高B处有两只猴子，如下图1，一只猴子爬下树走到离树20米处的池塘的A处；

另一只爬到树顶D后直接跃到A处，距离以直线计算，如果两只猴子所经过的距离相等，则这棵树高米?

2、长为4m的梯子搭在墙上与地面成45°

角，作业时调整为60°

角（如上图2所示），则梯子的顶端沿墙面升高了______m．

3．在平静的湖面上，有一支红莲，高出水面1米，一阵风吹来，红莲移到一边，花朵齐及水面，已知红莲移动的水平距离为2米，求这里的水深是米?

4、将一根24cm的筷子，置于底面直径为15cm，高8cm的圆柱形水杯中，如上图4所示，设筷子露在杯子外面的长度为hcm，则h的取值范围是（　　）．

A．h≤17cm　　　B．h≥8cm　　C．15cm≤h≤16cm　　D．7cm≤h≤16cm

如图，△ABC中，∠C＝90°

，D为AB的中点，E、F分别在AC、BC上，且DE⊥DF．

求证：

AE2＋BF2＝EF2．

6．已知：

如图，在正方形ABCD中，F为DC的中点，E为CB的四等分点且CE＝，

AF⊥FE．

7．已知△ABC中，a2＋b2＋c2＝10a＋24b＋26c－338，试判定△ABC的形状，并说明你的理由．

8．已知a、b、c是△ABC的三边，且a2c2－b2c2＝a4－b4，试判断三角形的形状．

9．如图，长方体的底面边长分别为1cm和3cm，高为6cm．如果用一根细线从点A开始经过四个侧面缠绕一圈到达点B，那么所用细线最短需要多长?

如果从点A开始经过四个侧面缠绕n圈到达点B，那么所用细线最短需要多长?

10、三角形的三边长为,则这个三角形是（）

（A）等边三角形（B）钝角三角形（C）直角三角形（D）锐角三角形.

11、如图，A市气象站测得台风中心在A市正东方向300千米的B处，以10千米/时的速度向北偏西60°

的BF方向移动，距台风中心200千米范围内是受台风影响的区域．

（1）A市是否会受到台风的影响？

写出你的结论并给予说明；

（2）如果A市受这次台风影响，那么受台风影响的时间有多长？

12、如图，某沿海开放城市A接到台风警报，在该市正南方向100km的B处有一台风中心，沿BC方向以20km/h的速度向D移动，已知城市A到BC的距离AD=60km，那么台风中心经过多长时间从B点移到D点？

如果在距台风中心30km的圆形区域内都将有受到台风的破坏的危险，正在D点休闲的游人在接到台风警报后的几小时内撤离才可脱离危险？

13、已知：

如图，∠B=∠D=90°

，∠A=60°

，AB=4，CD=2。

求：

四边形ABCD的面积。

14、如图，公路MN和公路PQ在点P处交汇，且∠QPN＝30°

，点A处有一所中学，AP＝160m。

假设拖拉机行驶时，周围100m以内会受到噪音的影响，那么拖拉机在公路MN上沿PN方向行驶时，学校是否会受到噪声影响？

请说明理由，如果受影响，已知拖拉机的速度为18km/h，那么学校受影响的时间为多少秒？

15、如图，在等腰△ABC中，∠ACB=90°

，D、E为斜边AB上的点，且∠DCE=45°

。

DE2=AD2+BE2。

（提示：

把△CAD旋转到BC外侧）

16、如下图1所示，△ABC是等腰直角三角形，AB=AC，D是斜边BC的中点，E、F分别是AB、AC边上的点，且DE⊥DF，若BE=12，CF=5．则线段EF的长为。

17、如上图2，在△ABC中，AB=13，BC=14，AC=15，则BC边上的高AD=。

18、如上图3，长方形ABCD中，AB=8，BC=4，将长方形沿AC折叠，点D落在点E处，则重叠部分△AFC的面积是。

19、在△ABC中，AB=15，AC=20，BC边上的高AD=12，则BC边的长为.

20、如上图，∠xoy=60°

，M是∠xoy内的一点，它到ox的距离MA为2。

它到oy的距离MB

为11。

则OM的长为。

21、在△ABC中，D是BC所在直线上一点，若AB=l0，BD=6，AD=8，AC=17，则△ABC的面积为。

22、在△ABC中，BC=1997，AC=1998，AB2=1997+1998，则△ABC是否为直角三角形？

为什么？

女女字旁（好妈奶）心心字底（想思念）23、已知△ABC的三边a、b、c，且a+b=17，ab=60，c=13,△ABC是否是直角三角形？

你能说明理由吗？

小树渐渐长高了。

24、木箱的长、宽、高分别为40dm、30dm和50dm，有一70dm的木棒，能放进去吗？

请说明理由。

我正忙着写作业呢！

（男）——（女）湿——（干）红——（绿）答案.　

妈妈一边洗手，一边说话。

A组13、解：

要在Rt△ABC的外部接一个合适的直角三角形，使得拼成的图形是一个等腰三角形，关键是腰与底边的确定。

要求在图中标明拼接的直角三角形的三边长，这需要用到勾股定理知识。

下图中的四种拼接方法供参考。

一面红旗一个朋友一对朋友一条木船一条小河

和风细雨万紫千红鸟语花香山清水秀蒙蒙细雨古往今来

ABAC式的词语

17、解析：

连结BM，根据勾股定理，在中，

.而在中，则根据勾股定理有

　.∴

又∵（已知），∴.在中，根据勾股定理有

　，　∴.

B组:

14、解析：

作AB⊥MN，垂足为B。

在RtΔABP中，∵∠ABP＝90°

，

∠APB＝30°

，AP＝160，∴AB＝AP＝80。

（30°

所对的直角边等于斜边的一半）

∵点A到直线MN的距离小于100m，∴这所中学会受到噪声的影响。

如图，假设拖拉机在公路MN上沿PN方向行驶到点C处学校开始受到影响，那么AC＝100（m），

由勾股定理得：

BC2＝1002-802＝3600，∴BC＝60。

同理，拖拉机行驶到点D处学校开始脱离影响，那么，AD＝100（m），BD＝60（m），∴CD＝120（m）。

拖拉机行驶的速度为:

18km/h＝5m/s　

t＝120m÷

5m/s＝24s。

答：

学校受影响的时间为24秒。

小松鼠从树上跳下来。

我从学校走出来。

（15题图）

足足字旁（跳跑）亻单人旁（休体何）20、提示，过A作AC⊥OX,交OM于D，作ME⊥AC于E，可求得AE=1，EC=MB=11，　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

得AC=12，再求AO，则可求得OM=14。