自考线性代数经管类公式汇总精髓版文档格式.docx
《自考线性代数经管类公式汇总精髓版文档格式.docx》由会员分享,可在线阅读,更多相关《自考线性代数经管类公式汇总精髓版文档格式.docx(51页珍藏版)》请在冰豆网上搜索。
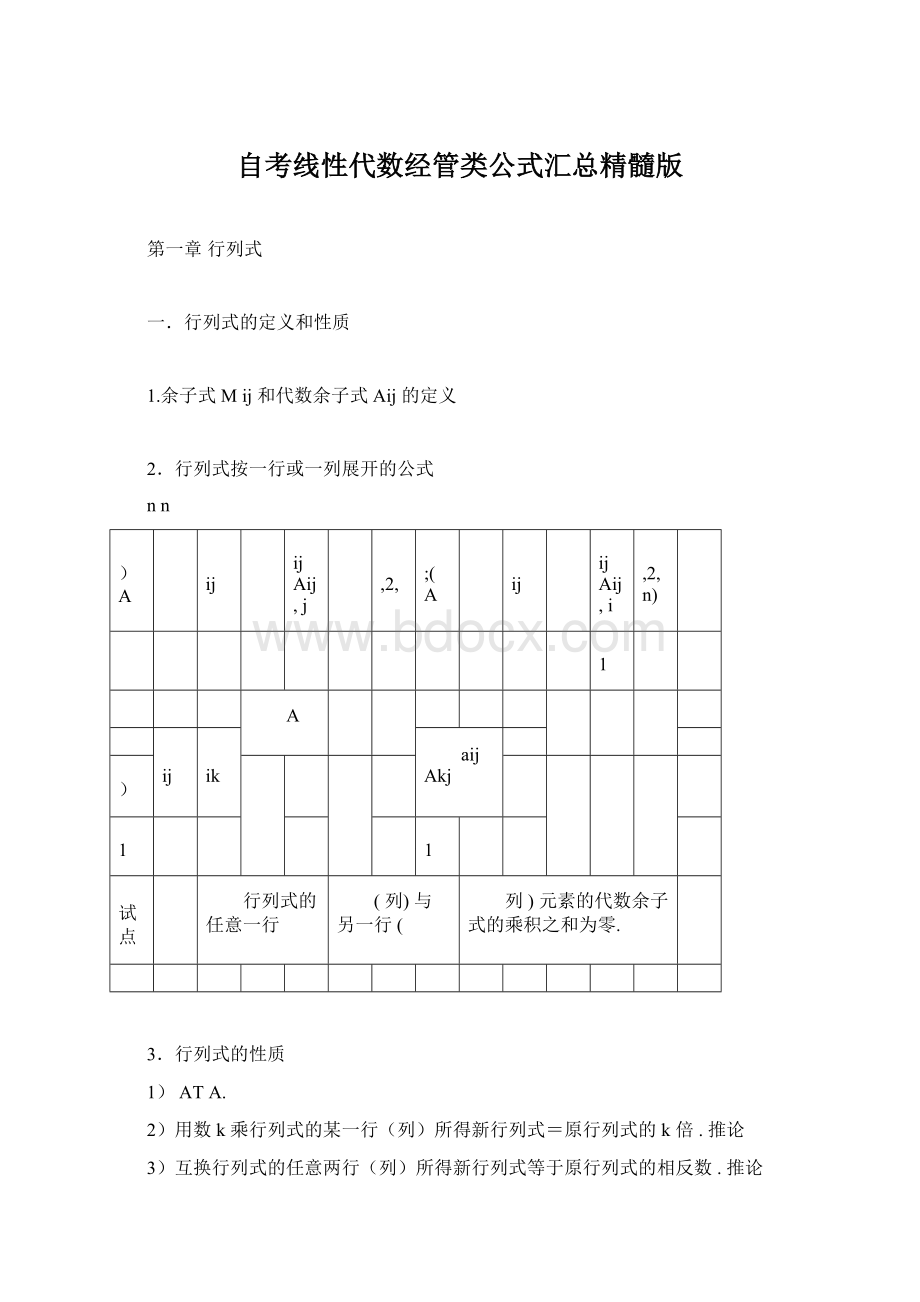
(列)与另一行(
列)元素的代数余子式的乘积之和为零.
3.行列式的性质
1)ATA.
2)用数k乘行列式的某一行(列)所得新行列式=原行列式的k倍.推论
3)互换行列式的任意两行(列)所得新行列式等于原行列式的相反数.推论
4)如果行列式中两行(列)对应元素成比例,则行列式值为0.
5)行列式可以按任一行(列)拆开.
6)行列式的某一行(列)的
k倍加到另一行(列)上,所得新行列式与原行列式的值相等
.
例设行列式a1
b1=1,
a1
c1
=2,则a1
b1
c1=(
3)
a2
b2
a2
c2
二.行列式的计算
1.二阶行列式和三角形行列式的计算.
2.对一般数字行列式,利用行列式的性质将其降阶以化成二阶行列式或三角形行列式的计算.
3.对行列式中有一行或一列中只有一个或两个非零元的情况,用这一行或一列展开.
4.行列式中各行元素之和为一个常数的类型.
5.范德蒙行列式的计算公式
123
23
3
100
20
例(性质4)249
49
9
200
40
0.
(1)
(1)
(2)
(2)
(1)(3)
367
67
7
300
60
例(各行元素之和为常数的行列式的计算技巧)
xaaax3a
aaax3a
a
D
axaax3a
xaa
xa
(x3a)(xa)3.
x
3a
例(行列式中有一行只有两个元素不为零的行列式的计算和三角形行列式的计算)
b
1)n1Mn1
an
(1)n1bn
Dn
=aA11bAn1=aM11+b(
x2
x3
2
4
8
例D(x)
中,x3项的系数A14(
1)51
(32)(42)(43)2
27
16
64
第二章矩阵
一、矩阵的概念
1.要弄清矩阵与行列式的区别
2.两个矩阵相等的概念
3.几种特殊矩阵(0矩阵,单位阵,三角阵,对角阵,数量阵)二、矩阵的运算
1.矩阵A,B的加、减、乘有意义的充分必要条件
2.矩阵运算的性质
比较矩阵运算(包括加、减、数乘、乘法等)的性质与数的运算性质的相同点和不同点(加法的交换律和结
合律;
乘法关于加法的分配律;
)重点是矩阵乘法没有交换律(由此产生了矩阵运算公式与数的运算的公式
的不同点.
(AB)2
A2+ABBAB2;
(AB)(A-B)
A2+BA-AB-B2;
(AB)k
ABAB
AB
AkBk;
E)2
A2
2AE
如果ABO,可能A
O,B
O.例如A
ABO.
B
都不为零,但
3.转置对称阵和反对称阵
1)转置的性质
B)T
AT
BT;
(
A)T
AT;
(ABC)T
CTBTAT
2)若
T
)
AA
A,则称A为对称(反对称)阵
例A为任意n阶矩阵,下列矩阵中为反对称矩阵的是(
B)
A.A
B.AAT
C.AAT
D.ATA
解析
AT)T
(AT)T
AT.故A
AT为对称阵.
AT).故A
AT为反对称阵.
(AAT)T
AAT.故AAT
为对称阵.同理
ATA也为对称阵.
4.方阵的行列式的性质
ATA;
A
nA;
ABAB;
Ak
Ak;
A11;
AAn1.
5.逆矩阵
1)方阵A可逆(也称非异,A满秩)的充分必要条件是
A0.
A11
A21
An1
当A可逆时,A1
1A.其中方阵A的伴随阵A的定义A
A12
A22
An2
。
A1n
A2n
Ann
d
特别
当ad
bc
时,
ad
c
重要公式
AA
AAAE;
A与A
1的关系
;
2)重要结论:
若
n阶方阵A,B满足AB
E,则A,B都可逆,且A1
B,B1
A.
3)逆矩阵的性质:
(A1)1
A;
当
0时,(A)1
1A1;
(AB)1
B1A1;
(AT)1
(A1)T;
A1
4)消去律:
设方阵
A可逆,且AB
AC(BA
CA),则必有B
C.(若不知A可逆,仅知A
0结论不一定成
立。
例设A为2阶可逆矩阵,且已知
(2A)
,则A=
解由
所以2A
故A
例(求逆矩阵的方法)设
求A1.
5
解方法1
A1
方法2
AE
(2)+(-2)
(1)
(3)+3
(1)
(3)
(2)
(2)
1(3)
例(若AB
E则A,B都可逆,且A1
A.)
已知A2
2A8EO,则(A
E)1
_____________。
解
由A2
2A8EO得A2
A3A3E5E
0,即(AE)(A3E)
5E,
即
E)(A3E)
E,故(A
1(A
3E).
例
设A是n阶方阵,且(A
E)2
O,证明A可逆?
.
证因为(AE)2
O,即A2
2A
E0,所以
A(A2E)E
故A可逆,且A1
(A2E).
设n阶方阵A满足Am
O,其中m为正整数,证明E
A可逆,且(EA)1
EAA2
Am1
分析
只要检查(E
A)(EAA2
Am1)
E即可
证
因为
(E
A)(E