机械原理课程设计连杆机构B4文档格式.docx
《机械原理课程设计连杆机构B4文档格式.docx》由会员分享,可在线阅读,更多相关《机械原理课程设计连杆机构B4文档格式.docx(17页珍藏版)》请在冰豆网上搜索。
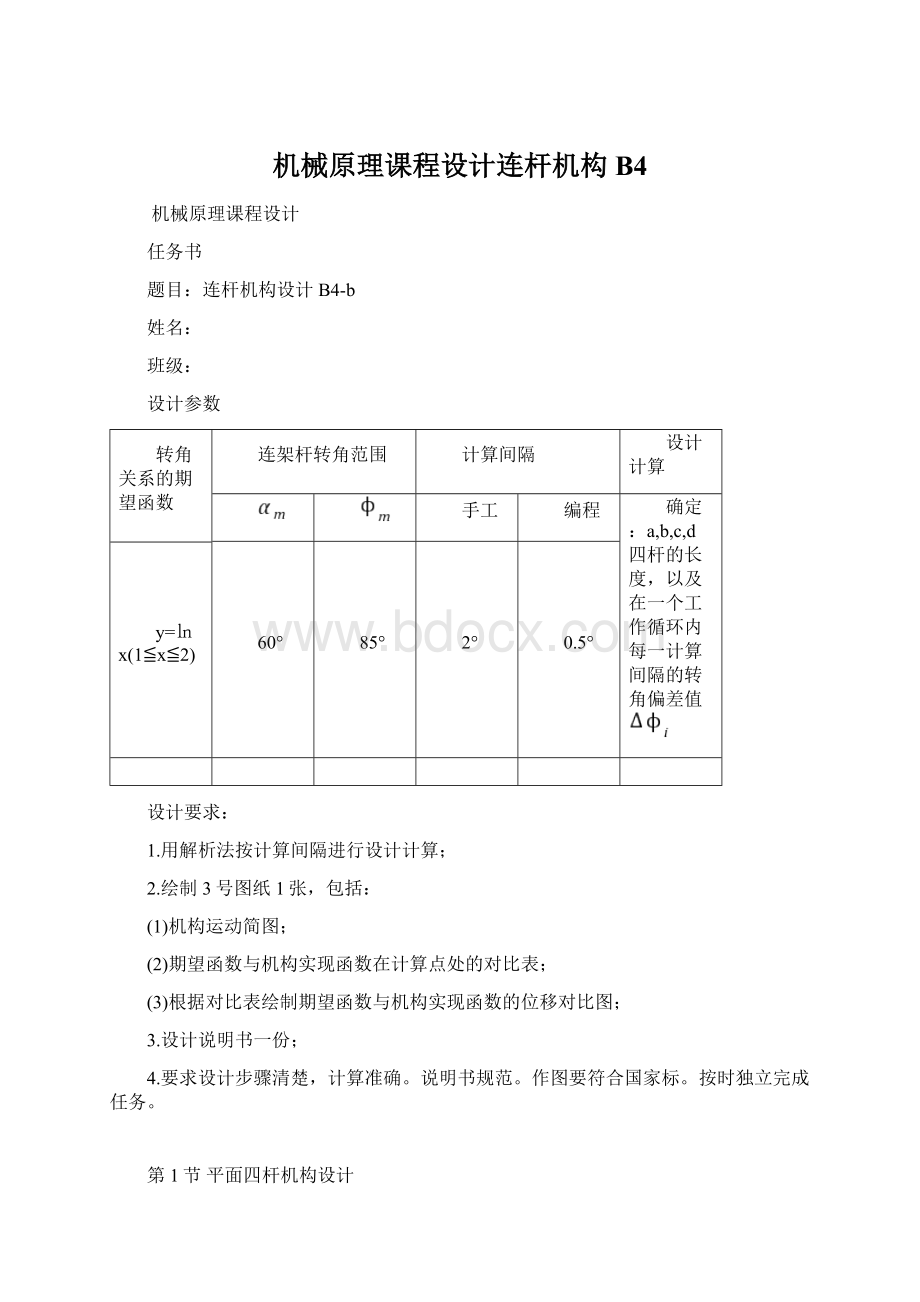
1.用解析法按计算间隔进行设计计算;
2.绘制3号图纸1张,包括:
(1)机构运动简图;
(2)期望函数与机构实现函数在计算点处的对比表;
(3)根据对比表绘制期望函数与机构实现函数的位移对比图;
3.设计说明书一份;
4.要求设计步骤清楚,计算准确。
说明书规范。
作图要符合国家标。
按时独立完成任务。
第1节平面四杆机构设计
1.1连杆机构设计的基本问题
连杆机构设计的基本问题是根据给定的要求选定机构的型式,确定各构件的尺寸,同时还要满足结构条件(如要求存在曲柄、杆长比恰当等)、动力条件(如适当的传动角等)和运动连续条件等。
根据机械的用途和性能要求的不同,对连杆机构设计的要求是多种多样的,但这些设计要求可归纳为以下三类问题:
(1)预定的连杆位置要求;
(2)满足预定的运动规律要求;
(3)满足预定的轨迹要求;
连杆设计的方法有:
解析法、作图法和实验法。
1.2作图法设计四杆机构
对于四杆机构来说,当其铰链中心位置确定后,各杆的长度
也就确定了。
用作图法进行设计,就是利用各铰链之间相对运动
的几何关系,通过作图确定各铰链的位置,从而定出各杆的长度。
根据设计要求的不同分为四种情况:
(1)按连杆预定的位置设计四杆机构
(2)按两连架杆预定的对应角位移设计四杆机构
(3)按预定的轨迹设计四杆机构
(4)按给定的急回要求设计四杆机构
1.3解析法设计四杆机构
在用解析法设计四杆机构时,首先需建立包含机构各尺度参数和运动变量在内的解析式,然后根据已知的运动变量求机构的尺度参数。
现有三种不同的设计要求,分别是:
(1)按连杆预定的连杆位置设计四杆机构
(2)按预定的运动轨迹设计四杆机构
(3)按预定的运动规律设计四杆机构
1)按预定的两连架杆对应位置设计
2)按期望函数设计
本次连杆机构设计采用解析法设计四杆机构中的按期望函数设计。
下面在第2节将对期望函数设计四杆机构的原理进行详细的阐述。
第2节设计介绍
2.1按预定的两连架杆对应位置设计原理
如下图所示:
设要求从动件3与主动件1的转角之间满足一系列的对应位置关系,即=i=1,2,…,n其函数的运动变量为由设计要求知、为已知条件。
有为未知。
又因为机构按比例放大或缩小,不会改变各机构的相对角度关系,故设计变量应该为各构件的相对长度,如取a/a=1,b/a=lc/a=m,d/a=n。
故设计变量l、m、n以及、的计量起始角、共五个。
如图所示建立坐标系Oxy,并把各杆矢量向坐标轴投影,可得
2-1
为消去未知角,将上式两端各自平方后相加,经整理可得
令=m,=-m/n,=,则上式可简化为:
2-2
式2-2中包含5个待定参数、、、、及,故四杆机构最多可以按两连架杆的5个对应位置精度求解。
2.2按期望函数设计
如上图所示,设要求设计四杆机构两连架杆转角之间实现的函数关系(成为期望函数),由于连架杆机构的待定参数较少,故一般不能准确实现该期望函数。
设实际实现的函数为月(成为再现函数),再现函数与期望函数一般是不一致的。
设计时应该使机构的再现函数尽可能逼近所要求的期望函数。
具体作法是:
在给定的自变量x的变化区间到内的某点上,使再现函数与期望函数的值相等。
从几何意义上与两函数曲线在某些点相交。
这些点称为插值结点。
显然在结点处:
故在插值结点上,再现函数的函数值为已知。
这样,就可以按上述方法来设计四杆机构。
这种设计方法成为插值逼近法。
在结点以外的其他位置,与是不相等的,其偏差为
偏差的大小与结点的数目及其分布情况有关,增加插值结点的数目,有利于逼近精度的提高。
但结点的数目最多可为5个。
至于结点位置分布,根据函数逼近理论有
2-3
试中i=1,2,…,3,n为插值结点数。
本节介绍了采用期望函数设计四杆机构的原理。
那么在第3节将
具体阐述连杆机构的设计。
第3节连杆机构设计
3.1连杆机构设计
设计参数表
注:
本次采用编程计算,计算间隔0.5°
3.2变量和函数与转角之间的比例尺
根据已知条件y=㏑x(1≦x≦2)为铰链四杆机构近似的实现期望函数,
设计步骤如下:
(1)根据已知条件,,可求得,。
(2)由主、从动件的转角范围=60°
、=85°
确定自变量和函数与转角之间的比例尺分别为:
3—1
3.3确定结点值
设取结点总数m=3,由式2-3可得各结点处的有关各值如表(3-1)所示。
表(3-1)各结点处的有关各值
1
1.067
0.065
4.02°
7.97°
2
1.500
0.405
30.0°
49.68°
3
1.933
0.659
55.98°
80.83°
3.4确定初始角、
通常我们用试算的方法来确定初始角、,而在本次连杆设计中将通过编程试算的方法来确定。
具体思路如下:
任取、,把、取值与上面所得到的三个结点处的、的值代入P134式8-17
从而得到三个关于、、的方程组,求解方程组后得出、、,再令=m,=-m/n,=。
然
求得后m,n,l的值。
由此我们可以在机构确定的初始值条件下找
到任意一位置的期望函数值与再现函数值的偏差值。
当
时,则视为选取的初始、角度满足机构的运动要求。
具体程序如下:
#include<
stdio.h>
math.h>
#definePI3.1415926
#definetPI/180
voidmain()
{
inti;
floatp0,p1,p2,a0,b0,m,n,l,a5;
floatA,B,C,r,s,f1,f2,k1,k2,j;
floatu1=1.0/60,u2=0.93/685,x0=1.0,y0=0.0;
floata[3],b[3],a1[6],b1[3];
FILE*p;
if((p=fopen("
d:
\\zdp.txt"
"
w"
))==NULL)
printf("
can'
topenthefile!
"
);
exit(0);
}
a[0]=4.02;
a[1]=30;
a[2]=55.98;
b[0]=7.97;
b[1]=49.68;
b[2]=80.83;
pleaseinputa0:
\n"
scanf("
%f"
&
a0);
pleaseinputb0:
b0);
for(i=0;
i<
3;
i++)
a1[i]=cos((b[i]+b0)*t);
a1[i+3]=cos((b[i]+b0-a[i]-a0)*t);
b1[i]=cos((a[i]+a0)*t);
p0=((b1[0]-b1[1])*(a1[4]-a1[5])-(b1[1]-b1[2])*(a1[3]-a1[4]))/
((a1[0]-a1[1])*(a1[4]-a1[5])-(a1[1]-a1[2])*(a1[3]-a1[4]));
p1=(b1[0]-b1[1]-(a1[0]-a1[1])*p0)/(a1[3]-a1[4]);
p2=b1[0]-a1[0]*p0-a1[3]*p1;
m=p0;
n=-m/p1;
l=sqrt(m*m+n*n+1-2*n*p2);
p0=%f,p1=%f,p2=%f,m=%f,n=%f,l=%f\n"
p0,p1,p2,m,n,l);
fprintf(p,"
\n"
5;
{printf("
pleaseinputoneangleoffives(0--60):
"
a5);
whentheangleis%f\n"
a5);
A=sin((a5+a0)*t);
B=cos((a5+a0)*t)-n;
C=(1+m*m+n*n-l*l)/(2*m)-n*cos((a5+a0)*t)/m;
j=x0+u1*a5;
A=%f,B=%f,C=%f,j=%f\n"
A,B,C,j);
s=sqrt(A*A+B*B-C*C);
f1=2*(atan((A+s)/(B+C)))/(t)-b0;
f2=2*(atan((A-s)/(B+C)))/(t)-b0;
r=(log(j)-y0)/u2;
k1=f1-r;
k2=f2-r;
r=%f,s=%f,f1=%f,f2=%f,k1=%f,k2=%f\n"
r,s,f1,f2,k1,k2);
\n\n"
结合课本P135,试取=86°
,=24°
时:
程序运行及其结果为:
p0=0.601242,p1=-0.461061,p2=-0.266414,m=0.601242,n=1.304040,l=1.938257
whentheangleis0.000000
r=0.000000,s=1.409598,f1=-125.595070,f2=-0.296147,k1=-125.595070,k2=-0.296147
whentheangleis4.020000
r=7.954308,s=1.538967,f1=-130.920624,f2=7.970002,k1=-138.874939,k2=0.015694
whentheangleis30.000000
r=49.732372,s=1.924767,f1=-152.252411,f2=49.680004,k1=-201.984787,k2=-0.052368
whentheangleis55.980000
r=80.838707,s=1.864505,f1=-161.643921,f2=80.830002,k1=-242.482635,k2=-0.008705
whentheangleis60.000000
r=85.018051,s=1.836746,f1=-162.288574,f2=84.909149,k1=-247.306625,k2=-0.108902
由程序运行结果可知:
当取初始角=86°
、=24°
时(=