函数恒成立问题参变分离法.docx

函数恒成立问题参变分离法.docx

《函数恒成立问题参变分离法.docx》由会员分享，可在线阅读，更多相关《函数恒成立问题参变分离法.docx（11页珍藏版）》请在冰豆网上搜索。

函数恒成立问题参变分离法

函数恒成立问题——参变分离法

学科

数学

课题名称

函数恒成立问题——参变分离法

周次

教学目标

教学重难点

函数恒成立问题——参变分离法

一、基础知识：

1、参变分离：

顾名思义，就是在不等式中含有两个字母时（一个视为变量，另一个视为参数），可利用不等式的等价变形让两个字母分居不等号的两侧，即不等号的每一侧都是只含有一个字母的表达式。

然后可利用其中一个变量的范围求出另一变量的范围

2、如何确定变量与参数：

一般情况下，那个字母的范围已知，就将其视为变量，构造关于它的函数，另一个字母（一般为所求）视为参数。

3、参变分离法的适用范围：

判断恒成立问题是否可以采用参变分离法，可遵循以下两点原则：

（1）已知不等式中两个字母是否便于进行分离，如果仅通过几步简单变换即可达到分离目的，则参变分离法可行。

但有些不等式中由于两个字母的关系过于“紧密”，会出现无法分离的情形，此时要考虑其他方法。

例如：

，等

（2）要看参变分离后，已知变量的函数解析式是否便于求出最值（或临界值），若解析式过于复杂而无法求出最值（或临界值），则也无法用参变分离法解决问题。

（可参见”恒成立问题——最值分析法“中的相关题目）

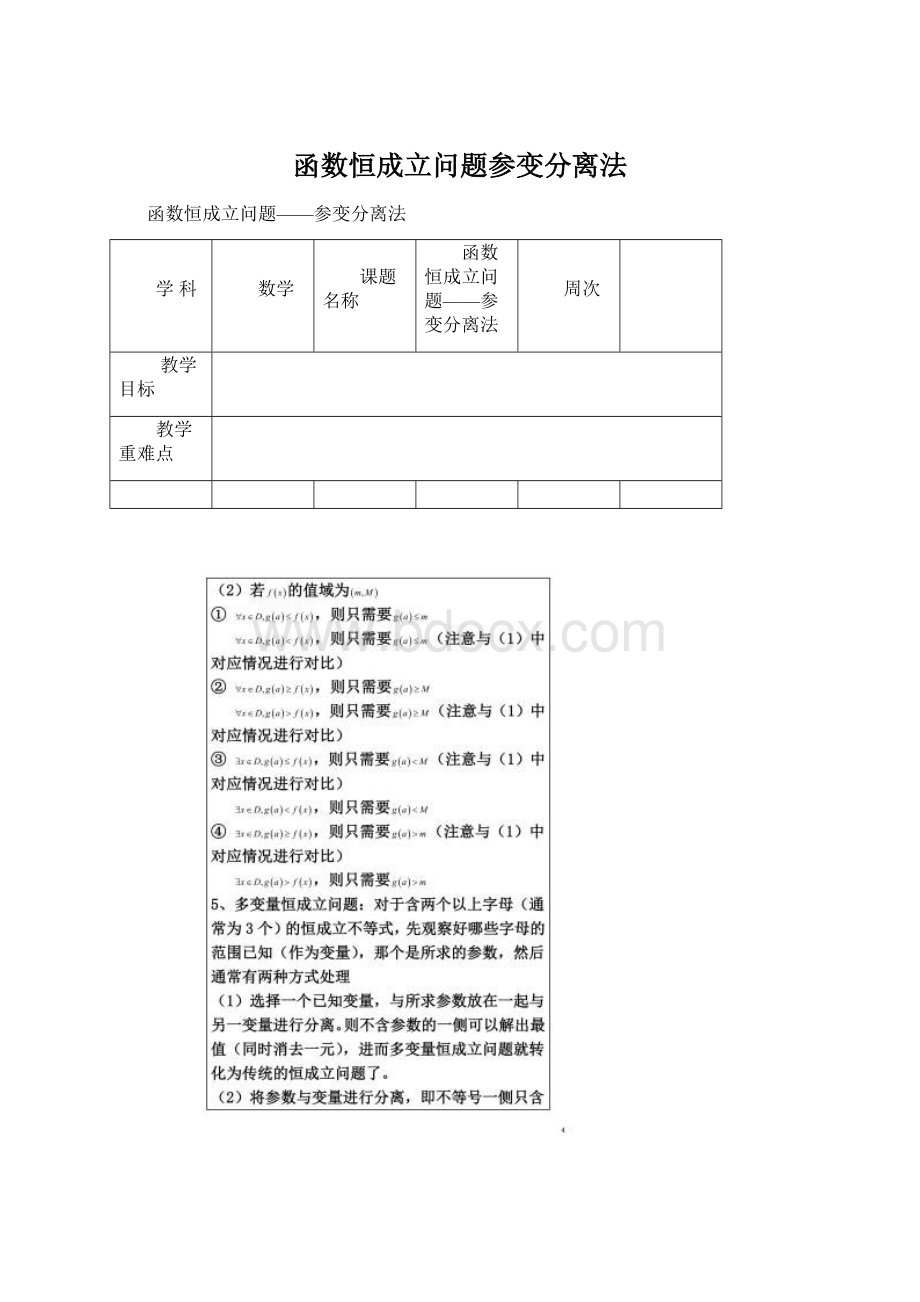
4、参变分离后会出现的情况及处理方法：

（假设为自变量，其范围设为，为函数；为参数，为其表达式）

（1）若的值域为

①，则只需要

，则只需要

②，则只需要

，则只需要

③，则只需要

，则只需要

④，则只需要

，则只需要

只需要，令

（导函数无法直接确定单调区间，但再求一次导即可将变为，所以二阶导函数的单调性可分析，为了便于确定的符号，不妨先验边界值）

，，（判断单调性时一定要先看定义域，有可能会简化判断的过程）

在单调递减，在单调递减

答案：

注意：

求导数的目的是利用导函数的符号得到原函数的单调性，当导函数无法直接判断符号时，可根据导函数解析式的特点以及定义域尝试在求一次导数，进而通过单调性和关键点（边界点，零点）等确定符号。

例3：

若对任意，不等式恒成立，则实数的范围是．

思路：

在本题中关于的项仅有一项，便于进行参变分离，但由于,则分离参数时要对的符号进行讨论，并且利用的符号的讨论也可把绝对值去掉，进而得到的范围，，当时，，而；当时，不等式恒成立；当时，，而

综上所述：

答案：

注意：

（1）不等式含有绝对值时，可对绝对值内部的符号进行分类讨论，进而去掉绝对值，在本题中对进行符号讨论一举两得：

一是去掉了绝对值，二是参变分离时确定不等号的是否变号。

（2）在求解析式最值时根据式子特点巧妙使用均值不等式，替代了原有的构造函数求导出最值的方法，简化了运算。

（3）注意最后确定的范围时是三部分取交集，因为是对的取值范围进行的讨论，而无论取何值，的值都要保证不等式恒成立，即要保证三段范围下不等式同时成立，所以取交集。

例4：

设函数，对任意的恒成立，则实数的取值范围是________________

思路：

先将不等式进行化简可得：

，即，便于进行分离，考虑不等式两边同时除以，可得：

，，

最小值，即解得：

答案：

注意：

本题不等式看似复杂，化简后参变分离还是比较容易的，从另一个角度看本题所用不等式为二次不等式，那么能否用二次函数图像来解决呢？

并不是一个很好的办法，因为二次项系数为关于的表达式且过于复杂，而对称轴的形式也不利于下一步的计算。

所以在解题时要注意观察式子的结构，能够预想到某种方法所带来的运算量，进而做出选择

例5：

若不等式对恒成立，则实数的取值范围是．

思路：

，令，对绝对值内部进行符号讨论，即，而在单调递增，在单调递减，可求出

答案：

例6：

设正数，对任意，不等式恒成立，则正数的取值范围是（）

思路：

先将放置不等号一侧，可得，所以，先求出的最大值，，可得在单调递增，在单调递减。

故，所以若原不等式恒成立，只需，不等式中只含，可以考虑再进行一次参变分离，，则只需，，

所以解得：

答案：

例7：

已知函数，若对于任意的，不等式恒成立，求实数的取值范围

思路：

含有参数，而为常系数函数，且能求出最值，所以以为入手点：

若恒成立，则只需。

可求出，进而问题转化为，恒成立，此不等式不便于利用参变分离求解，考虑利用最值法分类讨论解决

解：

恒成立只需

由得：

，令解得：

在单调递减，在单调递增

，恒成立

即只需

当时，令

则，与矛盾

当时，解得

在单调递增，在单调递减

综上所述：

注意：

（1）在例6，例7中对于多变量恒成立不等式，都是以其中一个函数作为突破口求得最值，进而消元变成而二元不等式，再用处理恒成立的解决方法解决。

（2）在本题处理恒成立的过程中，对令这个反例，是通过以下两点确定的：

①时估计函数值的变化，可发现当时，（平方比一次函数增长的快）②在选取特殊值时，因为发现时，已然为正数，所以只需前面两项相消即可，所以解方程，刚好符合反例的要求。

例8：

若不等式对任意正数恒成立，则正数的最小值是（）

A.B.C.D.

思路：

本题无论分离还是分离都相对困难，所以考虑将归至不等号的一侧，致力于去求表达式的最值：

，从入手考虑使用均值不等式：

，所以

答案：

B

注意：

（1）在多变量不等式恒成立问题上处理方式要根据不等式特点灵活选择合适的方法，本题分离与很方便，只是在求二元表达式最值上需要一定的技巧。

（2）本题在求的最大值时，还可以从表达式分子分母齐次的特点入手，同时除以（或）：

，在通过换元转化为一元表达式，再求最值即可。

例9：

已知函数，如果当时，不等式恒成立，求实数的取值范围.

思路：

恒成立不等式为,只需不等号两侧同时乘以即可进行参变分离，且由于,，也不存在不等号变号问题。

则可得：

只需即可，设，尝试利用导数求得最小值，

解：

即只需要

设

令（分子的符号无法直接判断，所以考虑再构造函数进行分析）

在单调递增

在单调递增

答案：

例10：

已知函数,若,且对任意恒成立,则的最大值为_________.

思路：

恒成立不等式，，令，则，考虑分子，在单调递增。

尽管不能够确定零点，但可以通过零点存在性定理大致的确定零点所在的位置。

，使得。

，同理，时，，所以在单调递减，在单调递增。

，因为即，

答案：

3

注意：

（1）本题的一个重要技巧在于对零点的“设而不求”，在求得单调增的前提下，判断的符号零点必不可少，但方程无法求出解。

那么卡在这一步是否要放弃重来？

不然。

可暂用一个变量来表示零点，再用特殊点的函数值将零点控制在一个小的范围内。

在本题中这种方法带来方法上的两个突破：

第一，能够判断的符号进而得到的符号，确定了的单调性，找到最小值。

第二，尽管不可求，但是本身自带一个方程，从而达到了一个对数与一次函数的转换。

对后面的化简有极大帮助

（2）若所求变量在整数集中取值，则求变量的值时不仅可利用等量关系，也可考虑求关于该变量的不等关系，再由其整数性选取符合条件的整数即可。