点线面之间位置关系复习教学案_精品文档Word文档下载推荐.doc

点线面之间位置关系复习教学案_精品文档Word文档下载推荐.doc

《点线面之间位置关系复习教学案_精品文档Word文档下载推荐.doc》由会员分享，可在线阅读，更多相关《点线面之间位置关系复习教学案_精品文档Word文档下载推荐.doc（24页珍藏版）》请在冰豆网上搜索。

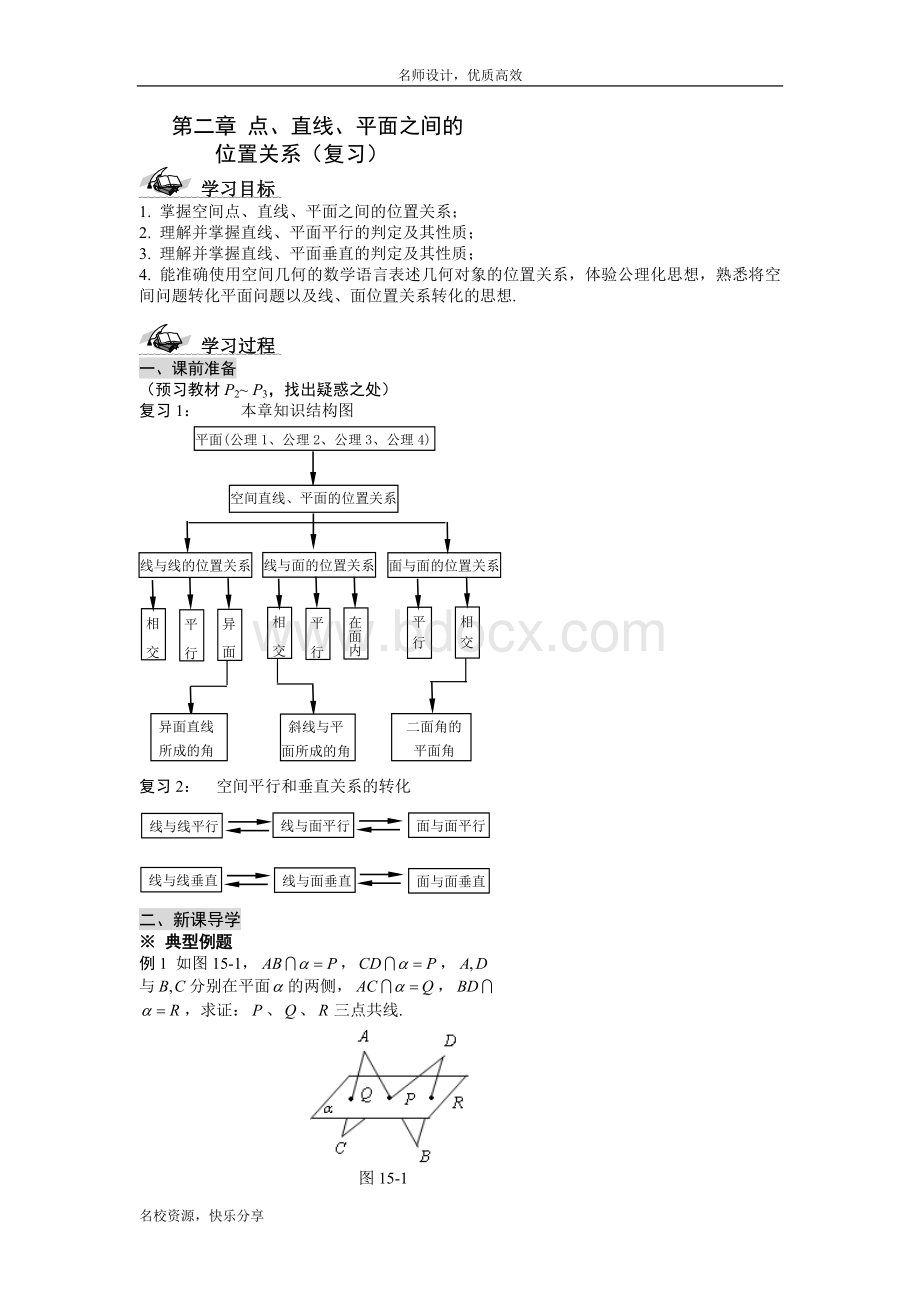
在面内

平行

相交

异面直线

所成的角

斜线与平

面所成的角

二面角的

平面角

复习2：

空间平行和垂直关系的转化

线与线平行

面与面平行

线与面平行

线与线垂直

线与面垂直

面与面垂直

二、新课导学

※典型例题

例1如图15-1，，，

与分别在平面的两侧，，

，求证：

、、 三点共线.

图15-1

例2如图15-2，在三棱锥P-ABC中，AC=BC=2，∠ACB=90°

，AP=BP=AB，PC⊥AC.

⑴求证：

PC⊥；

⑵求二面角B-AP-C的正切值；

⑶求点C到平面APB的距离.

图15-2

※动手试试

练1.证明：

两两相交且不过同一点的三条直线必在同一平面内.

练2.如图15-3，平面两两相交，为三条交线，且∥，证明：

∥，∥.

图15-3

练3.如图15-4，在中，°

，，

两点分别在上，使:

=:

=,，现将沿折成直二角角，求：

⑴异面直线与所成角的大小；

⑵二面角的正切值.

图15-4

三、总结提升

※学习小结

1.点、线、面的位置关系；

平行和垂直的证明；

角度的求解；

2.各种定理的灵活运用，转化思想的运用.

※知识拓展

欧氏几何古希腊数学家欧几里得在公元前300年完成了著作《几何原本》，共有十三卷，讲述了三角形全等条件、三角形边和角的大小关系、平行线理论、圆、内接和外切多边形、相似多边形理论、比例和算术的理论、立体几何知识，包含现代中学课程里初等几何的绝大部分内容，因此长期以来，人们都认为《几何原本》是两千多年来传播几何知识的标准教科书.属于《几何原本》内容的几何学，人们把它叫做欧几里得几何学，简称为欧氏几何.

学习评价

※自我评价你完成本节导学案的情况为（）.

A.很好B.较好C.一般D.较差

※当堂检测（时量：

5分钟满分：

10分）计分：

1.过平行六面体任意两条棱的中点作直线，其中与面平行的直线有（）.

A.4条B.6条C.8条D.12条

2.在正方体中，下列结论错误的是（）.

A.∥平面B.平面

C.D.与所成的角为°

3.在四棱锥的四个侧面中，直角三角形最多可有

（）.

A.1个B.2个C.3个D.4个

4.两个不重合的平面有公共点，则公共点的个数是

____________.

5.设直线，过平面外一点与、都成

°

角的直线有且只有________条.

课后作业

1.如图15-5，矩形ABCD和梯形BEFC所在平面互相垂直，∥CF，BCF=CEF=，AD=

，EF=2.

∥平面DCF；

⑵当的长为何值时，二面角的大小为？

图15-5

2.如图15-6所示，在正方体中，求证：

⑴平面；

⑵与平面的交点是的重心（三角形三条中线的交点）.

图15-6

陕西省宝鸡市金台区高一数学必修2质量检测试题（卷）2011.9

本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。

第Ⅰ卷1至2页。

第Ⅱ卷3至6页。

考试结束后.只将第Ⅱ卷和答题卡一并交回。

参考公式：

；

；

；

；

第Ⅰ卷（选择题共60分）

注意事项：

1．答第Ⅰ卷前，考生务必将姓名、准考号、考试科目用铅笔涂写在答题卡上。

2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案，不能答在试题卷上。

一、选择题：

本答题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1.一个平面内有无数条直线平行于另一个平面，那么这两个平面

A、一定平行B、一定相交C、平行或相交D、一定重合

2.两圆和的位置关系是

Ａ、相离　　　　Ｂ、相交　　　Ｃ、内切　　　　Ｄ、外切

3.从长方体一个顶点出发的三个面的面积分别为2、3、6，则它的体积为

A、6B、36C、D、2

4．若点P关于坐标平面xoy及y轴的对称点的坐标分别是（a,b,c）、（e,f,d）,则c与e的和为

A、7B、－7C、－1D、1

5．下列命题正确的是

A、过一点作一条直线的平行平面有无数多个

B、过一点作一直线的平行直线有无数条

C、过平面外一点，与该平面平行的直线有无数条

D、过两条平行线中的一条的任一平面均与另一条直线平行

6.若一条直线与两个平行平面中的一个平行，则这条直线与另一个平面的位置关系是

A、平行B、在平面内C、相交D、平行或在平面内

7.若直线与直线的交点位于第四象限，则实数的取值范围是

A、B、C、D、

8.已知是两条不同直线，是三个不同平面，以下有三种说法：

①若∥，∥，则∥；

②若⊥，∥，则⊥；

③若⊥，⊥，,则∥.

其中正确命题的个数是

A、3个 B、2个C、 1个 D、0个

9.已知平面α⊥平面β，α∩β=l，点A∈α，Al，直线AB∥l，直线AC⊥l，直线m∥α，m∥β，则下列四种位置关系中，不一定成立的是

A.AB∥m B.AC⊥m C.AC⊥β D.AB∥β

10.对两条不相交的空间直线和，必定存在平面，使得

A、B、

C、D、

11.经过圆的圆心C，且与直线垂直的直线方程是

A、B、

C、D、

12.若直线与圆有公共点，则

A． B．

C． D．

二、填空题：

本大题共6小题，每小题5分，共30分。

把本大题答案填在第Ⅱ卷题中横线上。

13.已知直线l通过直线和直线的交点，且与直线平行，则直线l的方程为.

14．在空间坐标系中，已知直角三角形ABC的三个顶点为A、B、C，则的值为.

15.已知直线a∥平面α，直线b在平面α内，则a与b的位置关系为

16．点P在直线上，O是坐标原点，则的最小值是_________．

17.三个平面能把空间分为部分.（填上所有可能结果）

18．下列命题中，所有正确的命题的序号是.

①一条直线和两条直线平行线中的一条垂直，则它也和另一条垂直；

②空间四点A、B、C、D，若直线AB和直线CD是异面直线，那么直线AC和直线BD也是异面直线；

③空间四点若不在同一个平面内，则其中任意三点不在同一条直线上；

④若一条直线l与平面内的两条直线垂直，则.

高一数学必修2质量检测试题（卷）2009.1

题号

二

三

总分

总分人

19

20

21

22

得分

复核人

第Ⅱ卷（非选择题）

本大题共6小题，每小题5分，共30分.把答案填在题中横线上.

13．;

14._________________.

15._________.16.

17.________________.18.__________________.

三、解答题：

本大题共4小题，共60分。

解答应写出文字说明、证明过程或演算步骤.

19．（本题满分15分）求经过三点A，B（）,C（0，6）的圆的方程，并指出这个圆的半径和圆心坐标.

20.（本题满分15分）如图，这是一个奖杯的三视图，

（1）请你说明这个奖杯是由哪些基本几何体组成的；

（2）求出这个奖杯的体积（列出计算式子，将数字代入即可，不必求出最终结果）.

21.（本题满分15分）已知：

四边形ABCD是空间四边形，E,H分别是边AB，AD的中点，F,G分别是边CB，CD上的点，且.

求证：

（1）四边形EFGH是梯形；

（2）FE和GH的交点在直线AC上.

22.（本题满分15分）已知圆C：

.

（1）写出圆C的标准方程；

（2）是否存在斜率为1的直线m，使m被圆C截得的弦为AB，且以AB为直径的圆过原点.若存在，求出直线m的方程;

若不存在,说明理由.

高一数学必修2质量检测参考答案2009.1

一、1.C2.Ｃ（p85练习题2（3）改）3.A（p45，练习题2改）

4．D（p90,练习题第3、4题改）5．C6.D（p33，,练习题2第2题改）

7.A8.A（复习题一8题改）9.C.（08海南宁夏卷文12）

10.B（08浙江卷文9）11.D（08广东卷文6）12.A（全国Ⅰ卷文10）

13.（写为也可）（p97,A组第10、11题改）

14．0；

15.平行或异面（p34,A组2题改）；

16．（08全国Ⅱ卷文3改）；

17.4，或6，或7，或8（p33,练习2，3题改）18．①②

解答应写出文字说明、证明过程或演算步骤。

19．（必修2，p80,例4改）

解：

设所求圆的方程为（2分）

由已知，点A，B（）,C（0，6）的坐标满足上述方程，分别代入方程，可得（8分）

解得：

于是得所求圆的