结构力学经典计算题.docx

结构力学经典计算题.docx

《结构力学经典计算题.docx》由会员分享，可在线阅读，更多相关《结构力学经典计算题.docx（32页珍藏版）》请在冰豆网上搜索。

结构力学经典计算题

结构力学经典计算题

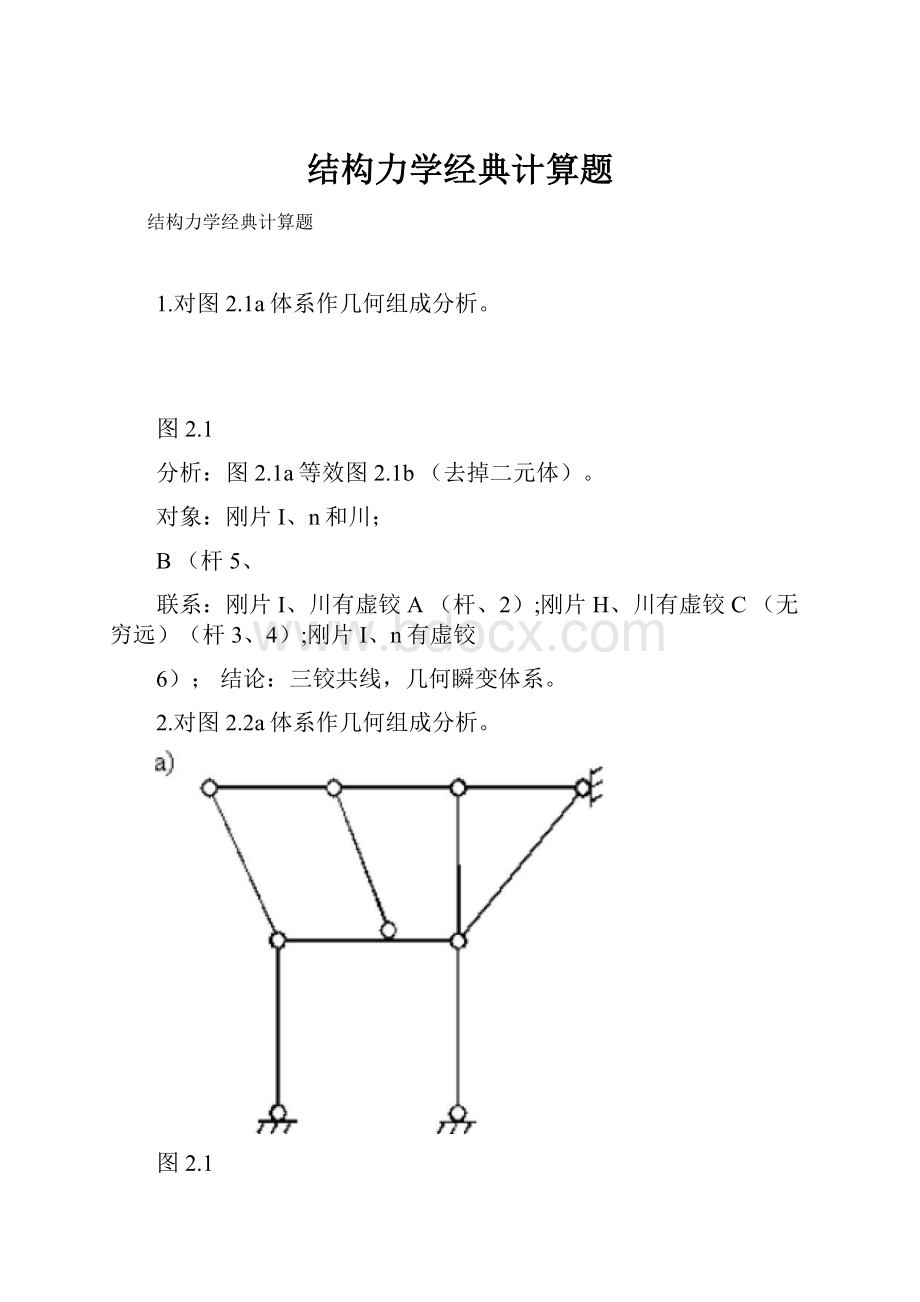
1.对图2.1a体系作几何组成分析。

图2.1

分析：

图2.1a等效图2.1b（去掉二元体）。

对象：

刚片I、n和川；

B（杆5、

联系：

刚片I、川有虚铰A（杆、2）;刚片H、川有虚铰C（无穷远）（杆3、4）;刚片I、n有虚铰

6）；结论：

三铰共线，几何瞬变体系。

2.对图2.2a体系作几何组成分析。

图2.1

分析：

去掉二元体（杆12、杆34和杆56图2.1b），等效图2.1c。

对象：

刚片I和n；

联系：

三杆：

7、8和9;

结论：

三铰不共线，无多余约束的几何不变体系。

fi

图2.3

分析：

图2.3a

对象：

刚片1（三角形原则）和大地n；

联系：

铰A和杆1;

结论：

无多余约束的几何不变体系。

对象：

刚片川（三角形原则）和大地n；

联系：

杆2、3和4;

结论：

无多余约束的几何不变体系。

第3章静定结构的受力分析典型题

1.求图3.1结构的内力图

1

2

B6.67

祐ET

仝

W

100

rrrrm

6d0

邂〔同-nO

Q圈（囿

图3.1

解

（1）支座反力（单位：

kN）

（2）内力（单位：

kN.m制）

取AD为脱离体：

=0Q肋二-100购％二-66.67城仪

,■

财皿二1040也化0皿=-160刼，阳》6667岳。

取结点D为脱离体：

%=%，為一％=6667^阪二篤一160城

取BE为脱离体:

@月=160孙，^=66.67^

取结点E为脱离体:

胚酹二-M曲二64C^M轉,Qsl二N甜二66.67EM

（3）内力图见图3.1b~d。

2.判断图3.2a和b桁架中的零杆。

图3.2

分析：

判断桁架零杆的常用方法是找出桁架中的L型结点和T型结点。

如果这两种结点上无荷载作用•那么L型纪点的

两杆及T型结点的非共线杆均为零杆。

解：

图3.2a：

考察结点C、D、E、I、K、L,这些结点均为T型结点，且没有荷载作用，故杆件CG、DJ、EH、IJ、KH、LF

均为零杆。

考察结点G和H,这两个结点上的两竖向链杆均已判断为零杆，故这两个结点的受力也已成为T型结点的情形.由

于没有荷载作用，故杆件AG、BH也为零杆。

整个结构共有8根零杆•如图3.2c虚线所示。

图3.2b:

考察结点D，为“K'型结点且无荷载作用，故:

•二二门；对称结构对称荷载（A支座处的水平反力为零），有

■，故杆件DE和DF必为零杆。

考察结点E和F,由于DE、DF已判断为零杆.故杆件AE、BF也是零杆。

整个结构共有四根零杆。

如图3.2d虚线所示。

》二¥-X）

3.图3.3a三铰拱为抛物线型，轴线方程为，试求截面K的内力。

耳!

76kNC>

图3.3

分析：

结构为一主附结构：

三铰拱ACB为基本部分，CD和CE分别为附属部分。

内力分析时先求出附属部分在铰C处的反力，再对三铰拱进行分析。

对附局部分CD、CE的计算相当于对两个简支梁的计算，在铰C处只产生竖向反力。

这样•基本部分三铰拱的计

算

就转化为在铰C作用竖向集中力。

解:

1）附属部分CD和CE。

CD和CE相当于C端支于三铰拱的简支梁，故C处竖向反力为,

v_12x6L

$广二—=7ki'j）

（f）

（2）基本部分ACB的反力

三铰拱ACB部分的受力如图3.3b所示，由：

■,V.■'I.」；y

］「=匚二启=（f）

取BC为隔离体：

】；兀二：

1y（kN）（三铰供整体：

：

」二「二賞LW（kN）（

（3）截面K的内力

a/4x4

tan—--y（Z-2xjyK二〒yx3x（12—％二占⑻）axI12

4x49

取AK为隔离体（图3.2c）

（上侧受拉）

==3x3x15+48x3-36x3=49.5（^）

ZX=0「厂刀；L；"o

——凡（。

根据水平、竖向和斜向的比例关系得到:

^=57x-L+36x

v13

2243

屈

（压力）

第4章静定结构的位移计算典型题

1.求图4.1a两跨静定梁的B左右截面的相对转角，各杆El=常数。

6*

B

心e}4e》4rn*2苗»

（b）WpS（kM.m）

分析：

梁只需考虑弯曲变形的影响；先绘结构在实际荷载以及虚拟单位荷载作用下的弯矩图，再用图乘法计算位移。

解:

（1）做MP和一T图，见图4.1b〜c。

（2）图乘法计算位移

%=-^（-30+y-150+80+30+20）=275

2.求图4.2a结构点B的水平位移。

EI1=1.2W5kN-m2,El2=1.8>105kNm2。

图4.2

解：

（1）做MP和一］图，见图4.2b〜c。

（2）图乘法计算位移

=—（^X18xl2x9-1x18x12x9）=—=0.0027^3

（I

Ely32Eg

3.结构仅在ACB部分温度升高t度，并在D处作用外力偶M，试求图4-24a所示刚架A、B两点间水平向的相对线位移，已知各杆EI为常数，a为线膨胀系数，h为截面高度.

分析：

ACB为静定结构的附属部分，该部分温度变化时对基本部分无影响，只需考虑外荷载的影响。

解:

（1）做MP和们图，见图4.2b〜c。

（2）图乘法计算位移

1z1M2.n减

.1jE=—（—_XSXXX_）X〜二一

二一一」（相对压缩）

第5章力法典型题

1.图6.1a结构，在固定支座A、B处同时顺时针方向转动单位位移后，得出的最后弯矩图（图6.2b）,

求铰支座C处的转角。

El=常数。

图6.1

解：

⑴基本结构图6.1c

（2）力法的方程

EI211El2112117

2.A端转动BA时的弯矩图见图6.2b，试校核该弯矩图的正确性。

a）

b）I（EIa/L）

分析:

本题易出错之处：

求

0（时漏了_.■1，即支座转动引起的转角

解：

（1）平衡校核：

取结点B为隔离体

pt

（2）变形校核:

C截面的转角作为检查对象，0c0。

取图6.2c为基本结构

&严刃耳他-另心-

E12I2I212I

（3）弯矩图正确

入=1cm用力法计算由此引起的

3图6.3a超静定桁架，CD杆由于制造误差使其实际长度比原设计长度缩短了结构内力。

已知各杆EA=2.7XI05kN。

•）廉坊梅及內力血

图6.3

分析：

超静定桁架由于制造误差引起的内力分析问题。

力法典型方程的自由项属于由制造误差引起的静定桁架的位移。

解：

（1）一次超静定，切开BC杆件代之以一对轴向力XI，得到图6.3b基本结构。

（2）X1=I单独作用下基本结构的内力图6.3b，基本结构在制造误差单独作用厂的内力为零。

f3「3

——

I55

冥6x2+（lxlxl0）x2

_1p56108

~EA{2525+2°

864

25EA

（3）力法典型方程求解

（Vi+瓦=0

4

-x

5

第6章位移法典型题

1.

图6.1a结构.BC杆刚度为无穷大。

用位移法计算，并作弯矩图和剪力图。

已知AB,CD杆的EI=常数。

分析：

该结构是具有刚性杆的结构。

由于刚性杆在结点B，C处均有水平约束，故只有一个竖向线位移Z1。

解：

（1）结构的基本未知量为刚性杆BC的竖向位移Z1（图6.1b）。

（2）设i=!

，写出结构在Z1及荷载共同作用下的杆端弯矩和杆端剪力为

^A£二财副二_了"2「胚如二胚加二

仏-#皿j

（3）取刚性杆BC为隔离体（6.1b）

却二他任-2宀g和十和m

（4）解位移方程：

7_PP

112i

（5）将Z1回代，绘弯矩图剪力图（图6.1c、d）

2.图6.2a结构，各杆EI=常数，不计轴向变形。

试求杆件AD和BD的内力。

分析:

图6.2

因不考虑各杆件的轴向变形，结点D只有角位移，没有线位移。

解：

基本未知量：

结点D的角位移Z1

位移法典型方程为:

荷载单独作用下的弯矩图（6.2b）。

结点D的力矩平衡：

■J-'oZ1=0,结点D没有角位移。

图6.2b的弯矩图为结构的最后弯矩图。

弯矩图6.2b

杆件AD，BD和CD的弯矩均为零，故剪力也为零，只可能有轴力。

图6.2c隔离体:

图6.3

解:

基本未知量为*o

基本体系及次〕图（图6.3b~c）。

系数和自由项为:

弯矩值的计算（弯矩图图6.3d）

%=—Q碍隅一Q吟汁斗轲二弓（3.4臀-0一片）Mm=（10卫阴-\吟翠％=（「039现-2、146丼

第7章渐近法典型题

1.用力矩分配法求图所示结构的弯矩图。

El=常数，M=40KN.m。

图7.1

解：

（1）利用对称性，取1/4结构计算（图7.1b）。

结点C

Scd=EI/L=EI,Scb=4XEI/L=2EI，所以^ce=1/3,®b=2/3

结点B

Sbc=Sba，所以qc=“a=1/2

弯矩分配见表1,M图见图7.1c。

表7.1弯矩分配传递过程

项目

A

B

C

E

AB

BA

BC

CB

CE

EC

分配系数

0.5

0.5

2/3

1/3

分配传递

10—

20

t10

-10/3—

-20/3

t-10/3

t10/3

5/6

5/3

5/3

t5/6

-5/18—

-5/9

5/18

t5/18

最后弯矩

10.8

21.8

18.2

3.6

3.6

3.6

2.图7.2a结构，支座A发生了转角0A=0.005rad的顺时针转动，支座B下沉了△=2.0cm，结构还受图示荷载

作用。

用力矩分配法计算，并作弯矩图。

己知各杆EI=2.0XI04kNm。

图7.2

分析：

力矩分配法：

该结构虽有支座位移，但结构本身并没有结点线位移未知量。

支座位移单独引起的杆端弯矩看成固端弯矩；

结构只有一个刚结点。

解：

（1）计算分配系数

Sba=4XEI/4=EI,Sbc=3XEI/6=EI/2

谭=2/3,丹=1/3

（2）计算固端弯矩和不平衡力矩

衢=4x—x0005-^x002-^^=120-180-30二-90（归血）朋4护8

护J1

叫c=―x0.02—x50=40-25=15（妊屁）申恥=芍0（上测）6’2

不平衡力矩（图7.2b），有MB=mBA+mBc—30=-105（kNm）

（3）分配和传递计算见表7.2。

表7.2弯矩分配传递过程

项目

AB

BA

BC

CB

分配系数

2/3

1/3

固端弯矩

-90

-90

15

-50

分配传递

35

70

35

0

最后弯矩

-55

-20

50

-50

（4）结构的弯矩图见图7.2c。

第8章影响线典型题

1.作图8.1a三铰刚架水平推力HA和内力Mdc,Qdc的影响线。

P=1在水平梁FG上移动。

P|P=1

3

a）

c）M■影响线

b）IL影响线

d）Q墨响线

图8.1

解：

（1）水平推力HA（向右为正）的影响线（单位：

kN）

（2）Mdc（下侧受拉为正）影响线（单位：

kN-m）

（3）Qdc影响线（单位：

kN）

其内力值的计算见表8.1。

影响线见图8.1b~d。

表8.1内力值的计算见表8.1

项目

作用点

内力值

项目

作用点

内力值

项目

作用点

内力值

HA

F

-1

Mdc

F

-0.25

Qdc

F

-1/6

D

0

D

0

D左

0

C

-3

C

0.75

D右

1

E

0

E

0

E

0

G

-1

G

-0.25

G

-1/6

2.图8.2a单跨超静定梁AB,跨度为•，其上作用单位移动荷载P=1。

求支座A处MA的影响线。

分析：

用力法求MA，即得到影响线的方程。

解：

基本体系图8.2b系数计算

力法方程求解

的+%=°1412Z3

绘影响线将110等分见图8.2e,各点的MA值（单位：

kN・m）见表8.2，影响线见图8.2f

表8.2MA值

位置

1/10

2/10

3/10

4/10

5/10

6/10

7/10

8/10

9/10

10/10

MA（-）

0.6

1.44

1.79

1.92

1.85

1.68

1.37

0.96

0.5

0

第9章矩阵位移法典型题

1.用矩阵位移法计算图9.1a连续梁，并画M图，El=常数。

12kN/w

J11M

1j

t:

16m\

a）

图9.6

解:

c）

4.8

单元定位向量XD=（01）T,唸=（12）T,

（2）将各单元刚度矩阵中的元素按单元定位向量在K中对号入座，得整体刚度矩阵

&2r

2i8i

（4）将整体刚度矩阵K和等效结点荷载

ra纠

!

■%

2i8r

82

卜=<

12

A

P代人基本方程

0

L.J

（5）求杆端力并绘制弯矩图（图9.6c）。

2.图9.2a结构，荷载只在

（1）,（3）杆上作用，已知

（1）,（3）杆在局部坐标系（杆件箭头方向）中的单元刚度矩阵均为（长度单位为m，角度单位为rad，力单位为kN）

杆件

（2）的轴向刚度为EA=1.5X06kN，试形成结构的整体刚度矩阵。

图9.2

解:

（1）结构的结点位移编号及局部坐标方向（杆件箭头方向）见图9.1b。

（2）单元

（1）,（3）的局部与整体坐标方向一致，故其在整体坐标系中的单元刚度矩阵与局部坐标系中的相同。

（3）桁架单元

（2）的刚度矩阵

桁架单元只有轴向的杆端力和杆瑞位移,

（3）桁架单元

（2）的刚度矩阵

桁架单兀只有轴向的杆端力和杆瑞位移，

■0

00

0

0

3750

0

fe>]=

0

0

00

00

0

0

0

-3750

0

0

00

0

（3）定位向量

单元

（1）：

｛呼［000

12

单元

（2）：

0卜［124

5F

单元（3）：

沪卜［000

45

（4）整体刚度矩阵

500

0

0

0

12+375

-24

[蚪=

0

-24

64

0

0

0

0

「3乃

0

0

0

0

00

-3750

00

xlO

00

3750

00

0

0

〔〕_

0

-375

0

0

0

0

xlO

500

0

0

0

12+375

-24

0

-24

64

EI

500

0

0

0

0

0

0

387

-24

0

-375

0

0

-24

64

0

0

0

xlO5

0

0

0

500

0

0

0

-375

0

0

387

-24

0

0

0

0

-24

64_

3.求图9.3a结构整体刚度矩阵。

各标

相同，不考轴向变形。

a）

A

t9t

图9.3

解：

（1）单元结点编号（图9.8b）

b）

DQ-

B

T7T

TFT

（2）单元的定位向量

—（0051）T■—（0054）

汁一（5354）T「（5200）

（3）

单元刚度矩阵

（4）

（4）整体刚度矩阵

AE1

5

L

5

4

门257

65/

\2E1

6EI~

F

广

户

'lr\

65/

AEl

6应

AEl

ri2

l-

ri2

IJ

5

4

5

J

4

1.判断图10.1自由度的数量

第10章结构动力计算典型题

图10.1

2.列出图10.2a结构的振动方程，并求出自振频率。

El=常数。

b）c）

解：

挠度系数:

Alxixix2x!

+lx2/x：

xV=

刃222322232

51324SI-u

——x2/x—X—X—二

E12222

8£7

质点m的水平位移y为由惯性力和动荷载共同作用引起:

■V；.'T:

:

'。

自振频率:

3.图10.3a简单桁架，在跨中的结点上有集中质量m。

若不考虑桁架自重，并假定各杆的EA相同，试求自振频

率。

图10.3

分析：

结构对称，质量分布对称，所以质点m无水平位移，只有竖向位移，为单自由度体系。

4.简支梁，跨度a,抗弯刚度EI，抗弯截面模量Wz。

跨中放置重量为G转速n的电动机•离心力竖直分量

。

若不计梁重，试求动力系数、最大动位移及最大动应力。

解:

（2）最大动位移:

⑶最大动应力:

叽=%+mq=制岐+%町诟+劭

ml=2m2=m,El=常数，质点ml上

5.求图10.4a体系的自振频率和主振型，作振型图并求质点的位移。

已知

作用突加荷载

图10.4

解：

（1）频率方程

4腐1一4几叫

禹戶1①2%-—

（2）挠度系数

务二

4

3EI

Aa

2EI

7

Y2E1

（3）解方程求自振频率

（4）求主振型

（5）振型分解

\1

_1

1_

0】

>=

712

九一

i

!

■=

-044

46

%」

（6）求广义质量和广义矩阵

（7）求正则坐标

必）・\（1cos

突加荷载时’；■•

ri

F

帀10）=r2（1-8釦

144F

2战吠

£1

F

i）t（f）-尺[l-cosdi4）=

wo;

0.37F”、

（8）求质点位移：

血皿）+川）

旳©=-0.44加）+4.6%（。

6.用能量法求图10.5梁具有均布质量m=q/8的最低频率。

已知：

位移形状函数为:

咖唸附“曲1

图10.5

解：

（1）计算公式:

加[厂0）]%_血仗肌谕

（*W?

必+二强冒『两卩W13必+二忒

mi=0

（2）积分计算:

a

B'

0

a.

^（1-1.25,0.4）=3.13x10-^

宀+2十5音