仿真系统时间类型定义.docx

仿真系统时间类型定义.docx

《仿真系统时间类型定义.docx》由会员分享，可在线阅读，更多相关《仿真系统时间类型定义.docx（19页珍藏版）》请在冰豆网上搜索。

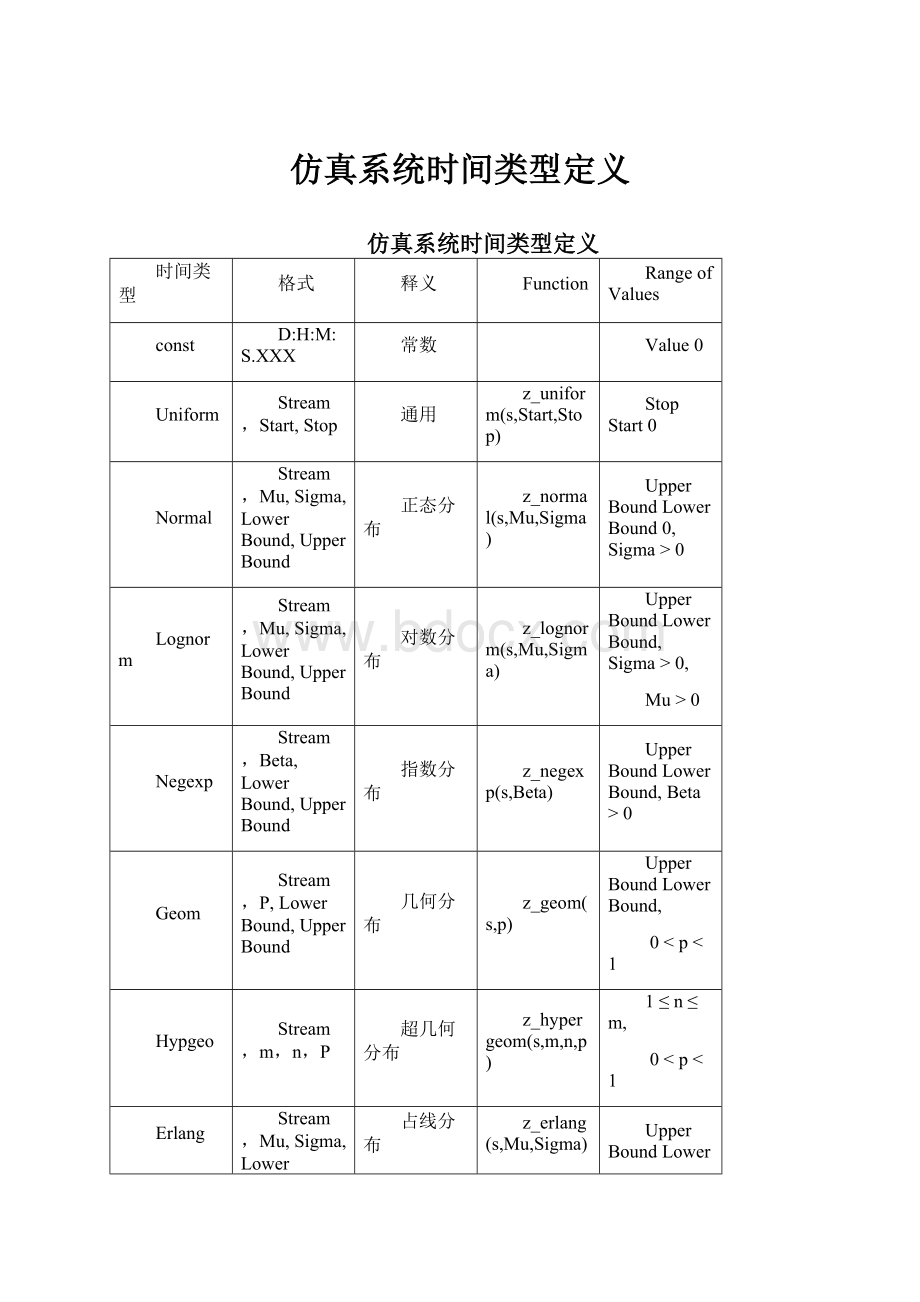
仿真系统时间类型定义

仿真系统时间类型定义

时间类型

格式

释义

Function

RangeofValues

const

D:

H:

M:

S.XXX

常数

Value0

Uniform

Stream，Start,Stop

通用

z_uniform（s,Start,Stop）

StopStart0

Normal

Stream，Mu,Sigma,LowerBound,UpperBound

正态分布

z_normal（s,Mu,Sigma）

UpperBoundLowerBound0,Sigma>0

Lognorm

Stream，Mu,Sigma,LowerBound,UpperBound

对数分布

z_lognorm（s,Mu,Sigma）

UpperBoundLowerBound,Sigma>0,

Mu>0

Negexp

Stream，Beta,LowerBound,UpperBound

指数分布

z_negexp（s,Beta）

UpperBoundLowerBound,Beta>0

Geom

Stream，P,LowerBound,UpperBound

几何分布

z_geom（s,p）

UpperBoundLowerBound,

0

Hypgeo

Stream，m，n，P

超几何分布

z_hypergeom（s,m,n,p）

1≤n≤m,

0

Erlang

Stream，Mu,Sigma,LowerBound,UpperBound

占线分布

z_erlang（s,Mu,Sigma）

UpperBoundLowerBound,Sigma>0

Weibull

Stream，Alpha,Beta,LowerBound,UpperBound

韦伯分布

z_weibull（s,Alpha,Beta）

UpperBoundLowerBound,Alpha>0,

Beta>0

Triangle

Stream，c,a,b

三角分布

z_triangle（s,c,a,b）

0≤a

Binomial

Stream，n,p

二项式分布

z_binominal（s,n,p）

n>0,

0

Poisson

Stream，Lamda

泊松分布

z_poisson（s,Lambda）

Lambda>0

Gamma

Stream，Beta,LowerBound,UpperBound

Gamma分布

z_gamma（s,Alpha,Beta）

UpperBoundLowerBound0,Alpha>0,

Beta>0

Beta

Stream，Alpha1,Alpha2

Beta分布

z_beta（s,Alpha1,Alpha2）

Alpha1>0,Alpha2>0

dEmp

Stream，Table[time,real]

离散经验

z_demp（s,Table）

Stream1

cEmp

Stream，Table[time,time,real]

连续经验

z_cemp（s,Table）

Stream1

Emp

Stream，Table[real，…]Column

简单经验

z_emp（s,Table,column）

Stream1

Formula

公式

DistributionFunctions

YoucancreaterandomnumberswithobjectsoftypeGeneratorandVariablesofdatatypetimeaswellaswiththefunctionsdescribedbelow,whichreturnrandomnumbersaccordingtothedesireddistribution.

你可以根据需要的数据分布形态，使用下面所述的针对时间变量的类型生成器，生成任意数值。

Theargumentsstandsfortherandomnumberstreamandisofdatatypeinteger.AllotherargumentsaretheargumentsofthecorrespondingdistributionfunctionasdescribedunderStatisticalDistributions.Theyalleitherareofdatatyperealorinteger.

Function

Resultsinthe

z_beta（s,Alpha1,Alpha2）

betadistribution

z_binominal（s,n,p）

binominaldistribution

z_cemp（s,Table）

steadyempiricaldistribution

z_demp（s,Table）

discreteempiricaldistribution

z_emp（s,Table,column）

primitiveempiricaldistribution

z_erlang（s,Mu,Sigma）

Erlangdistribution

z_gamma（s,Alpha,Beta）

gammadistribution

z_geom（s,p）

geometricdistribution

z_hypergeom（s,m,n,p）

hypergeometricdistribution

z_lognorm（s,Mu,Sigma）

lognormaldistribution

z_negexp（s,Beta）

exponentialdistribution

z_normal（s,Mu,Sigma）

normaldistribution

z_poisson（s,Lambda）

Poissondistribution

z_triangle（s,c,a,b）

triangulardistribution

z_uniform（s,Start,Stop）

uniformdistribution

z_weibull（s,Alpha,Beta）

Weibulldistributi

Type

Usage:

.Type:

=;

TheattributeTypedefinesthetypeofastatisticaldistributionfortheattributenamed.Attribute_pathdesignatesanattributeofdatatypetimeoracustomattributeofdatatyperandtime.

Distribution

NameineM-PlantEnglish/German

Constantnumber

Const/Konst

Uniformdistribution

Uniform/Gleich

Normaldistribution

Normal/Normal

Lognormaldistribution

Lognorm/Lognorm

Exponentialdistribution

Negexp/Negexp

Geometricdistribution

Geom/Geom

Hypergeometricdistribution

Hypgeo/Hypgeo

Erlangdistribution

Erlang/Erlang

Weibulldistribution

Weibull/Weibull

Triangulardistribution

Triangle/Dreieck

Binomialdistribution

Binomial/Binomial

Poissondistribution

Poisson/Poisson

Gammadistribution

Gamma/Gamma

Betadistribution

Beta/Beta

Discreteempiricaldistribution

dEmp/dEmp

Continuousempiricaldistribution

cEmp/cEmp

Primitiveempiricaldistribution

Emp/Emp

Formula

Formula/Formel

Type-dependentdistribution

List（Type）/Liste（Typ）

List-dependentdistribution（ParallelProc）

List（Place）/Liste（Platz）

Example:

singleProc.proctime.Type:

="uniform";

Thedifferentdistributionshavedifferentattributes.Youcansetthese:

∙WiththemethodsetParam.

∙WiththemethodsetTypeAndAttr.

∙Bydirectassignmentstotheattribute.

Example:

singleProc.proctime.Mu:

=0.50;

singleProc.proctime.Sigma:

=0.1;

Assignargumentsaccordingtothislist:

Distribution

SetofArguments

RangeofValues

Const

Value

Value0

Uniform

Stream,Start,Stop

StopStart0

Normal

Stream,Mu,Sigma,LowerBound,UpperBound

UpperBoundLowerBound0,Sigma>0

Lognorm

Stream,Mu,Sigma,LowerBound,UpperBound

UpperBoundLowerBound,Sigma>0,Mu>0

Negexp

Stream,Beta,LowerBound,UpperBound

UpperBoundLowerBound,Beta>0

Geom

Stream,p,LowerBound,UpperBound

UpperBoundLowerBound,0

Hypgeo

Stream,m,n,p

1≤n≤m,0

Erlang

Stream,Mu,Sigma,LowerBound,UpperBound

UpperBoundLowerBound,Sigma>0

Weibull

Stream,Alpha,Beta,LowerBound,UpperBound

UpperBoundLowerBound,Alpha>0,Beta>0

Triangle

Stream,c,a,b

0≤a

Binomial

Stream,n,p

n>0,0

Poisson

Stream,Lambda

Lambda>0

Gamma

Stream,Alpha,Beta,LowerBound,UpperBound

UpperBoundLowerBound0,Alpha>0,Beta>0

Beta

Stream,Alpha1,Alpha2

Alpha1>0,Alpha2>0

dEmp

Stream,List

Stream1

cEmp

Stream,List

Stream1

Emp

Stream,List,Column

Stream1

Formula

Formula

List（Type）

List

List（Place）

List

数学基础

NORMDIST正态分布

返回指定平均值和标准偏差的正态分布。

此函数在统计方面应用范围广泛（包括假设检验）。

语法

NORMDIST（x,mean,standard_dev,cumulative）

X  是需要计算其分布的数值。

Mean  分布的算术平均值。

Standard_dev  分布的标准偏差。

Cumulative  为一逻辑值，指明函数的形式。

如果cumulative为TRUE，则NORMDIST返回累积分布函数；如果为FALSE，则返回概率密度函数。

说明

∙如果mean或standard_dev为非数字型，则NORMDIST返回错误值#VALUE!

。

∙如果standard_dev≤0，则NORMDIST返回错误值#NUM!

。

∙如果mean=0，standard_dev=1，且cumulative=TRUE，则NORMDIST返回标准正态分布，即NORMSDIST。

∙正态分布密度函数（cumulative=FALSE）的计算公式如下：

∙如果cumulative=TRUE，则公式为从负无穷大到公式中给定的X的积分。

示例

X

Mean

StdDev

公式

说明（结果）

42

40

1.5

=NORMDIST（[X],[Mean],[StdDev],TRUE）

在指定的参数条件下的累积分布函数值（0.908789）

42

40

1.5

=NORMDIST（[X],[Mean],[StdDev],FALSE）

在指定的参数条件下的概率密度函数值（0.10934005）

LOGNORMDIST对数累积分布

返回x的对数累积分布，其中ln（x）是服从参数mean和standard_dev的正态分布。

使用此函数可以分析经过对数变换的数据。

语法

LOGNORMDIST（x,mean,standard_dev）

X  是用于计算函数的数值。

Mean  ln（x）的平均值。

Standard_dev  ln（x）的标准偏差。

说明

∙如果任一参数是非数字型，则LOGNORMDIST返回错误值#VALUE!

。

∙如果x≤0或standard_dev≤0，则LOGNORMDIST返回错误值#NUM!

。

∙对数累积分布函数的计算公式如下：

示例

X

Mean

StdDev

公式

说明（结果）

4

3.5

1.2

=LOGNORMDIST（[X],[Mean],[StdDev]）

在指定的参数条件下4的对数累积分布函数值（0.039084）

EXPONDIST指数分布

返回指数分布。

使用EXPONDIST可以建立事件之间的时间间隔模型，如银行自动提款机支付一次现金所花费的时间。

例如，可以使用函数EXPONDIST来确定这一过程最长持续一分钟的发生概率。

语法

EXPONDIST（x,lambda,cumulative）

X  函数的数值。

Lambda  参数值。

Cumulative  是一逻辑值，指出提供的指数函数的形式。

如果cumulative为TRUE，则EXPONDIST返回累积分布函数；如果为FALSE，则它返回概率密度函数。

说明

∙如果x或lambda为非数字型，则EXPONDIST返回错误值#VALUE!

。

∙如果x<0，则EXPONDIST返回错误值#NUM!

。

∙如果lambda≤0，则EXPONDIST返回错误值#NUM!

。

∙概率密度函数的计算公式如下：

∙累积分布函数的计算公式如下：

示例1

公式

说明（结果）

=EXPONDIST（0.2,10,FALSE）

概率指数分布函数（1.353353）

示例2

X

Lambda

公式

说明（结果）

0.2

10

=EXPONDIST（[X,][Lambda],TRUE）

累积指数分布函数（0.864665）

HYPGEOMDIST超几何分布

返回超几何分布。

在给定样本容量、样本总体成功次数和样本总体容量时，HYPGEOMDIST返回样本取得给定成功次数的概率。

使用HYPGEOMDIST可解决有限总体的问题，其中每个观察值或为成功或为失败，且其中给定样本容量的每一个子集有相等的发生概率。

语法

HYPGEOMDIST（sample_s,number_sample,population_s,number_population）

Sample_s  样本中成功的次数。

Number_sample  样本容量。

Population_s  样本总体中成功的次数。

Number_population  样本总体容量。

说明

∙所有参数都将被截尾取整。

∙如果任一参数为非数字型，则HYPGEOMDIST返回错误值#VALUE!

。

∙如果sample_s<0或sample_s大于number_sample或population_s中的较小值，则HYPGEOMDIST返回错误值#NUM!

。

∙如果sample_s小于0或（number_sample-number_population+population_s）中的较大值，则HYPGEOMDIST返回错误值#NUM!

。

∙如果number_sample<0或number_sample>number_population，则HYPGEOMDIST返回错误值#NUM!

。

∙如果population_s<0或population_s>number_population，则HYPGEOMDIST返回错误值#NUM!

。

∙如果number_population<0，则HYPGEOMDIST返回错误值#NUM!

。

∙超几何分布的计算公式如下：

式中：

x=sample_s

n=number_sample

M=population_s

N=number_population

HYPGEOMDIST用于在有限样本总体中进行不退回抽样的概率计算。

示例

抽样器里有20块巧克力。

其中8块是焦糖的，其余12块是果仁的。

如果随机选出4块，下面函数返回正好有一块是焦糖的概率。

Sample_s

Number_sample

Population_s

Number_Population

公式

说明（结果）

1

4

8

20

=HYPGEOMDIST（[Sample_s],[Number_sample],[Population_s],[Number_Population]）

样本和样本总体的超几何分布（0.363261）

WEIBULL分布

返回韦伯分布。

使用此分布可以进行可靠性分析，例如计算设备失效的平均时间。

语法

WEIBULL（x,alpha,beta,cumulative）

X  用于计算函数的数值。

Alpha  分布参数。

Beta  分布参数。

Cumulative  决定函数的形式。

说明

∙如果x、alpha或beta为非数字型，则WEIBULL返回错误值#VALUE!

。

∙如果x<0，则WEIBULL返回错误值#NUM!

。

∙如果alpha≤0或beta≤0，则WEIBULL返回错误值#NUM!

。

∙韦伯累积分布函数的计算公式如下：

∙韦伯概率密度函数的计算公式如下：

∙当alpha=1时，WEIBULL返回指数分布：

示例

X

Alpha

Beta

公式

说明（结果）

105

20

100

=WEIBULL（[X],[Alpha],[Beta],TRUE）

在指定的参数条件下韦伯累积分布函数（0.929581）

105

20

100

=WEIBULL（[X],[Alpha],[Beta],FALSE）

在指定的参数条件下韦伯概率密度函数（0.035589）

BINOMDIST一元二项式分布

返回一元二项式分布的概率值。

函数BINOMDIST适用于固定次数的测试或试验，当任何试验的结果仅包含成功或失败两种情况，当试验是独立试验，且当在整个试验过程中成功的概率固定不变。

例如，函数BINOMDIST可以计算三个婴儿中两个是男孩的概率。

语法

BINOMDIST（number_s,trials,probability_s,cumulative）

Number_s  是试验中成功的次数。

Trials  是独立试验的次数。

Probability_s  是每次试验中成功的概率。

Cumulative  是一逻辑值，用于确定函数的形式。

如果cumulative为TRUE，则函数BINOMDIST返回累积分布函数，即最多存在number_s次成功的概率；如果为FALSE，则返回概率密度函数，即正好存在number_s次成功的概率。

说明

∙Number_s和trials将被截尾取整。

∙如果number_s、trials或probability_s为非数字型，则BINOMDIST返回错误值#VALUE!

。

∙如果number_s<0或number_s>试验次数，则BINOMDIST返回错误值#NUM!

。

∙如果probability_s<0或probability_s>1，则BINOMDIST返回错误值#NUM!

。

∙二项式概率密度函数的计算公式如下：

其中：

等于COMBIN（n,x）。

注释  此处的COMBIN函数用于说明由BINOMDIST函数所用的数学公式。

它并非可以在列表中使用的函数。

累积二项式分布函数的计算公式如下：

示例

number_s

trials

probability_s

公式

说明（结果）

6